题目内容
 (2010?南平模拟)(强化班学生做)如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1,E的大小为0.5×103V/m,B1大小为0.5T.第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,微粒经过y轴上的N点并与y轴正方向成60°角的方向飞出.M点的坐标为(0,-10),N点的坐标为(0,30),不计微粒的重力,g取10m/s2.求:
(2010?南平模拟)(强化班学生做)如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1,E的大小为0.5×103V/m,B1大小为0.5T.第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,微粒经过y轴上的N点并与y轴正方向成60°角的方向飞出.M点的坐标为(0,-10),N点的坐标为(0,30),不计微粒的重力,g取10m/s2.求:(1)请分析判断匀强电场E1的方向并求出微粒的运动速度v;
(2)匀强磁场B2的大小为多大;
(3)B2磁场区域的最小面积为多少?
分析:带电粒子在电场与磁场共同作用下做直线运动,则可得洛伦兹力与电场力相平衡.当经过磁场B2区域一段时间后,微粒经过y轴上的N点并与y轴正方向成60°角的方向飞出,粒子在磁场B2区域做匀速圆周运动,若要求出B2磁场区域的最小面积,则且带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,从N点射出夹角相同.所以运动圆弧与直线MP及N点的速度反方向直线相切.
解答:解:(1)粒子在电场与磁场中做直线运动,速度会引起洛伦兹力的变化,因此微粒必做匀速直线运动,所以洛伦兹力与电场力相平衡.则有
B1qv=qE
解之得:v=
=
m/s=103m/s,
根据左手定则可得运动的正电荷所受洛伦兹力方向为:垂直于初速度方向向上,所以电场力的方向与洛伦兹力方向相反,即垂直于速度方向向下.
(2)粒子在磁场B2区域内做一段圆弧运动,画出微粒的运动轨迹如图.则有:微粒做圆周运动的向心力由洛伦兹力提供,
即Bqv=m
 ,
,
再 由几何关系可知粒子在第一象限内做圆周运动的半径为 R=
m
解之得 B2=
T.
(3)由图可知,磁场B2的最小区域应该分布在图示的矩形PACD内.
由几何关系易得PD=2Rsin60°=0.2m
PA=R(1-cos60°)=
m
所以,所求磁场的最小面积为S=PD×PA=0.2×
m2=
m2.
B1qv=qE
解之得:v=
| E |
| B1 |
| 0.5×103 |
| 0.5 |
根据左手定则可得运动的正电荷所受洛伦兹力方向为:垂直于初速度方向向上,所以电场力的方向与洛伦兹力方向相反,即垂直于速度方向向下.
(2)粒子在磁场B2区域内做一段圆弧运动,画出微粒的运动轨迹如图.则有:微粒做圆周运动的向心力由洛伦兹力提供,
即Bqv=m
| v2 |
| R |
 ,
,再 由几何关系可知粒子在第一象限内做圆周运动的半径为 R=
| ||
| 15 |
解之得 B2=
| ||
| 2 |
(3)由图可知,磁场B2的最小区域应该分布在图示的矩形PACD内.
由几何关系易得PD=2Rsin60°=0.2m
PA=R(1-cos60°)=
| ||
| 30 |
所以,所求磁场的最小面积为S=PD×PA=0.2×
| ||
| 30 |
| ||
| 150 |
点评:当带电粒子在电场与磁场中做直线运动时,由于洛伦兹力由速度决定,所以粒子必做匀速直线运动.当粒子进入磁场时,仅受洛伦兹力做匀速圆周运动,由几何关系可确定磁感应强度.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: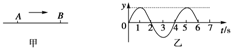 (2010?南平模拟)一列简谐横波以1m/s的速度沿绳子由A向B传播,质点A、B间的水平距离x=3m,如图甲所示.若t=0时质点A刚从平衡位置开始向上振动,其振动图象如图乙所示,则B点的振动图象为( )
(2010?南平模拟)一列简谐横波以1m/s的速度沿绳子由A向B传播,质点A、B间的水平距离x=3m,如图甲所示.若t=0时质点A刚从平衡位置开始向上振动,其振动图象如图乙所示,则B点的振动图象为( )