题目内容
19. 轻小滑轮P用一根轻绳系在天花板上的O点,重物A被绕过滑轮P的轻绳悬挂,物体B放置在粗糙的水平桌面上,O′是三根轻绳的结点,bO′水平,aO′、bO′与cO′的夹角如图所示.整个装置处于静止状态,不计轻绳与滑轮之间的摩擦,重力加速度g=10m/s2,若轻绳OP的张力为40$\sqrt{3}$N,则下列说法正确的是( )
轻小滑轮P用一根轻绳系在天花板上的O点,重物A被绕过滑轮P的轻绳悬挂,物体B放置在粗糙的水平桌面上,O′是三根轻绳的结点,bO′水平,aO′、bO′与cO′的夹角如图所示.整个装置处于静止状态,不计轻绳与滑轮之间的摩擦,重力加速度g=10m/s2,若轻绳OP的张力为40$\sqrt{3}$N,则下列说法正确的是( )| A. | 重物C的质量为1kg | B. | OP与竖直方向的夹角为60° | ||
| C. | 重物A的质量为4kg | D. | 桌面对B物体的摩擦力为20$\sqrt{3}$N |
分析 对滑轮分析,根据共点力平衡条件并结合正交分解法求解A的重力和OˊP的拉力;对点O′,同样根据三力平衡条件并结合正交分解法列式求解O′b的拉力和O′C的拉力;最后对B受力分析,求解桌面对B物体的摩擦力.
解答 解:因轻绳aOˊ和aA的拉力大小相等,由对称性,OP应在∠OˊPA的角平分线上,且2Tacos30°=Tp,故Ta=40N,即A的质量为4kg.
结点Oˊ平衡,故Tacos60°=Tc=Gc,所以Gc=20N,又Tasin60°=Tb=f,所以$f=20\sqrt{3}N$.选项C、D正确.
故选:CD
点评 本题关键是灵活选择研究对象,多次受力分析并根据平衡条件列平衡方程分析,对于多力平衡,通常采用正交分解法分析,不难.

练习册系列答案
相关题目
14. 如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
 如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )| A. | 箭射到靶的最短时间为$\frac{d}{{v}_{2}}$ | |
| B. | 箭射到靶的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ | |
| C. | 运动员应在到达A点前瞄准靶心放箭 | |
| D. | 运动员应在到达A点时瞄准靶心放箭 |
6.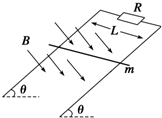 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )| A. | P=2mgvsin θ | |
| B. | P=3mgvsin θ | |
| C. | 当导体棒速度达到$\frac{v}{2}$时加速度大小为$\frac{g}{2}$sin θ | |
| D. | 在速度达到2v以后匀速运动的过程中,R上产生的焦耳热等于拉力所做的功 |
 图a是显示微小形变的装置,图b是测量万有引力恒量的实验装置,两个实验都采用了放大思想方法.在图b中,刻度尺与平面镜的距离越远(填“远”或“近”),越容易观察.
图a是显示微小形变的装置,图b是测量万有引力恒量的实验装置,两个实验都采用了放大思想方法.在图b中,刻度尺与平面镜的距离越远(填“远”或“近”),越容易观察.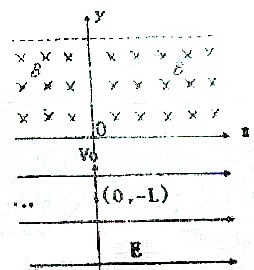 如图所示,坐标空间中有场强为E=$\frac{m{v}_{0}^{2}}{qL}$的匀强电场和磁感应强度为B的匀强磁场,x轴为两种场的分界面,图中虚线为磁场区域的上边界,现有一束质量为m、电荷量为q的带正电粒子从电场中坐标位置(O,-L)处,以初速度v0沿y轴正方向开始运动,不计粒子重力,已知量为:m,q,v0,B,L.求:
如图所示,坐标空间中有场强为E=$\frac{m{v}_{0}^{2}}{qL}$的匀强电场和磁感应强度为B的匀强磁场,x轴为两种场的分界面,图中虚线为磁场区域的上边界,现有一束质量为m、电荷量为q的带正电粒子从电场中坐标位置(O,-L)处,以初速度v0沿y轴正方向开始运动,不计粒子重力,已知量为:m,q,v0,B,L.求: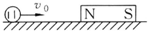 如图所示,在光滑水平面上固定一条形磁铁,有一小球以一定的初速度向磁铁方向运动,如果发现小球做减速运动,则小球的材料可能是( )
如图所示,在光滑水平面上固定一条形磁铁,有一小球以一定的初速度向磁铁方向运动,如果发现小球做减速运动,则小球的材料可能是( )