题目内容

已知某星球的质量是地球质量的81倍，半径是地球半径的9倍．在地球上发射一颗卫星，其第一宇宙速度为7.9km/s，则在某星球上发射一颗人造卫星，其发射速度最小是多少？
分析：建立模型：卫星绕地球做匀速圆周运动，地球对卫星的万有引力提供向心力．推广到其他球星．根据此模型，利用比例法求星球上发射人造卫星最小发射速度．
解答：解：设地球质量为M1，半径为R1；某星球的质量为M2，半径为R2
    由万有引力定律得：G
Mm
R 2
=m
v 2
R 

    可得：v =
GM 
R 

故地球和该星球第一宇宙速度之比为：
v1
v2
=
M1?R2
R1?M2
=
9
81
=
1
3

则在该星球上发射人造卫星速度至少为：v2=3v1=23.7km/s
答：在该星球上发射一颗人造卫星，其发射速度最小是23.7km/s．
点评：本题是卫星类型问题，关键是要建立物理模型，运用万有引力定律和向心力知识，加上数学变换来求解．
练习册系列答案
相关题目
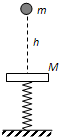精英家教网（A）如图所示，一轻弹簧竖直放置在地面上，下端固定，上端连接一质量为M的水平钢板，处于静止状态．现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞，碰撞后瞬间小球与钢板的速度大小相同．已知M=3m，不计空气阻力，重力加速度g取=10m/s2．则小球与钢板第一次碰撞后瞬间，钢板速度的大小为
 
 m/s；碰撞前后小球的动量变化量大小为
 
kg?m．
（B）某星球的质量是地球的2倍，其半径是地球的
12
．若不计其他星球的影响，该星球的第一宇宙速度是地球上第一宇宙速度的
 
倍，某物体在该星球表面上所受重力是在地球表面上所受重力的
 
倍．
（2011?上海模拟）一个在地球上走时正确的摆钟放到某星球表面上使用，经过1h的时间却在摆钟上读到走过的时间是0.4h．（取地球表面重力加速度g=10m/s2，空气阻力不计．）
（1）求该星球表面附近的重力加速度g’；
（2）已知该星球的半径与地球半径之比为R星：R地=1：4，求该星球的质量与地球质量之比M星：M地．
（3）若身高1.6m的宇航员在地球上跳高时能跃过1.6m高的横杆，在该星球表面以地球表面时同样的速度起跳，能跃过多高的横杆？（设宇航员站立时的重心在离脚0.8m处，跃过横杆时重心与杆等高．）
宇航员在地球表面以一定的初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间4t小球落回原处．（取地球表面重力加速度g地=10m/s2，阻力不计）
（1）求该星球表面附近的重力加速度g星；
（2）已知该星球的半径与地球半径之比为R星：R地=1：4，求该星球的质量与地球质量之比M星：M地；
（3）已知地球的第一宇宙速度是7.9km/s，求该星球的第一宇宙速度．
（A）如图所示，一轻弹簧竖直放置在地面上，下端固定，上端连接一质量为M的水平钢板，处于静止状态．现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞，碰撞后瞬间小球与钢板的速度大小相同．已知M=3m，不计空气阻力，重力加速度g取=10m/s2．则小球与钢板第一次碰撞后瞬间，钢板速度的大小为______ m/s；碰撞前后小球的动量变化量大小为______kg?m．
（B）某星球的质量是地球的2倍，其半径是地球的
1
2
．若不计其他星球的影响，该星球的第一宇宙速度是地球上第一宇宙速度的______倍，某物体在该星球表面上所受重力是在地球表面上所受重力的______倍．
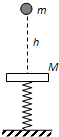
精英家教网
（A）如图所示，一轻弹簧竖直放置在地面上，下端固定，上端连接一质量为M的水平钢板，处于静止状态．现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞，碰撞后瞬间小球与钢板的速度大小相同．已知M=3m，不计空气阻力，重力加速度g取=10m/s2．则小球与钢板第一次碰撞后瞬间，钢板速度的大小为     m/s；碰撞前后小球的动量变化量大小为    kg?m．
（B）某星球的质量是地球的2倍，其半径是地球的．若不计其他星球的影响，该星球的第一宇宙速度是地球上第一宇宙速度的    倍，某物体在该星球表面上所受重力是在地球表面上所受重力的    倍．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网