题目内容
【题目】如图所示，水平放置的圆筒绕其中心对称轴OO′匀速转动，桶壁上P处有一小圆孔，桶壁很薄，桶的半径R=2m，当圆孔正上方h=3.2m处有一小球由静止开始下落，已知圆孔的半径略大于小球的半径。已知小球刚好能从孔中进入圆筒，并且与圆筒不发生碰撞离开圆筒。求
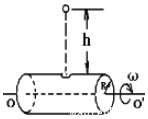
（1）小球在圆桶中运动的时间？
（2）圆筒转动的角速度是多大？（空气阻力不计，g取10m/s2）。
【答案】（1）0.4s；（2）
（k=1，2，3，…）；
【解析】
（1）据自由落体运动规律，有：
，解得：t1=0.8s，
h+R=
，解得：t2=1.2s，故小球在圆通中运动的时间△t=t2-t1=0.4s；
（2）根据小球在圆筒中运动时间与圆通自转的时间相等，则有θ=ω△t=（2k-1）π（k=1，2，3，…），解得：ω=
（k=1，2，3，…）；
练习册系列答案
相关题目
