题目内容
18.质绳跨过光滑轻质滑轮与物体B相连接,B的质量M=1kg,绳绷直时B离地面有一定高度.在t=0时刻,无初速度释放B,由固定在A上的速度传感器得到的数据绘出的A沿斜面向上运动的v-t图象如图乙所示,若B落地后不反弹,g取10m/s2,sin37°=0.6,cos37°=0.8,
(1)B下落的加速度大小为多少?
(2)A沿斜面向上运动的过程中,绳的拉力对A做的功为多少?
(3)A的质量M=0.5kg,A与斜面间的动摩擦因数μ为多少?
(4)0~0.75s内摩擦力对A做的功是多少?
分析 (1)AB具有相同的加速度,由题中v-t图象可得加速度.
(2)对B由牛顿第二定律可得绳的拉力,进而可得对A的功.
(3)由牛顿第二定律可得A受到的摩擦力,进而可得A与斜面的摩擦因数.
(4)根据牛顿第二定律可求得物体的质量;再由功的公式可得摩擦力做的功.
解答 解:(1)AB具有相同的加速度,由图可知B的加速度为:$a=\frac{2}{0.5}m/{s}^{2}=4m/s$2.
(2)、设绳的拉力为T,对B由牛顿第二定律:Mg-T=Ma,
解得:T=Mg-Ma=1×10-1×4=6N,
AB位移相同则由图可知A上升阶段,B的位移为:$x=\frac{2×0.5}{2}m=0.5m$
故绳的拉力对A做功为:W=Fx=6×0.5J=3J,
(3)由图可知后0.25s时间A的加速度为:$a′=\frac{△v′}{△t′}=\frac{2}{0.25}m/{s}^{2}=8m/{s}^{2}$
此过程A只受摩擦力和重力:
μmgcos+mgsinθ=ma′
解得:$μ=\frac{a′-gsinθ}{gcosθ}=\frac{8-10×sin37°}{10×cos37°}=0.25$
(4)前0.5s内A受到重力.支持力.摩擦力和拉力的作用,沿斜面的方向:
T-mgsinθ-μmgcosθ=ma
代入数据得:m=0.5kg,
全程位移为:
$s=\frac{1}{2}×2×0.75m=0.75m$
故摩擦力做功为:
Wf=-μmgcosθs=-0.25×0.5×10×0.8×0.75J=-0.75J
答:(1)B下落的加速度大小为4m/s2;
(2)A沿斜面向上运动的过程中,绳的拉力对A做的功为3J;
(3)A的质量M=0.5kg,A与斜面间的动摩擦因数μ为0.25;
(4)0~0.75s内摩擦力对A做的功是-0.75J.
点评 本题考查牛顿第二定律、功的计算及图象的分析问题,要注意正确选择研究对象,注意沿绳进行分析求解,选择正确的物理规律即可求解.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
①两位同学首先进行了如图甲所示的实验,将一根轻质弹簧竖直挂起,在弹簧的另一端挂上一个已知质量为m的小铁球,稳定后测得弹簧的伸长量为d.
| 次数 | M/kg | |v22-v12|/m2s-2 | E/J | F/N | W/J |
| 1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | E3 | 1.22 | W3 |
| 4 | 1.00 | 2.40 | 1.20 | 2.42 | 1.21 |
| 5 | 1.00 | 2.84 | 1.42 | 2.66 | 1.43 |
③B同学完成步骤①后,接着进行了如图丙所示的实验:将弹簧放在水平桌上,一端固定在竖直的墙上,另一端被小铁球压缩,测得压缩量为x,释放弹簧后,小铁球从高为h的桌面上水平抛出,抛出的水平距离为L.
(1)A、B两位同学进行如图甲所示的实验目的是为了确定什么物理量,这个物理量是弹簧的劲度系数k,请用m,d,表示的物理量k=$\frac{mg}{d}$.
(2)如果Ep=$\frac{1}{2}$kx2成立,那么:
A同学测出的物理量x与d、H的关系式是x=$\sqrt{2dH}$;
B同学测出的物理量x与d、h、L的关系式是x=L$\sqrt{\frac{d}{2h}}$.

| A. | 三个质点的位移相等 | B. | 三个质点的平均速度相等 | ||
| C. | 沿路径3运动的质点的位移最大 | D. | 10 s是时刻 |
 小球从空中自由下落,与水平地面相碰后弹到空中某一高度,其速度-时间图象如图所示,则由图可知下列判断正确的是( )
小球从空中自由下落,与水平地面相碰后弹到空中某一高度,其速度-时间图象如图所示,则由图可知下列判断正确的是( )| A. | 小球下落的加速度为5m/s2 | B. | 小球下落的高度为1m | ||
| C. | 小球能弹起的最大高度为0.45m | D. | 0-0.8s内小球的位移为1.7m |
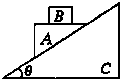 如图所示,光滑固定斜面C倾角为θ,质量均为m的两物块A、B一起以某一初速沿斜面向上做匀减速直线运动.已知物块A上表面是水平的,则在该减速运动过程中,下列说法正确的是( )
如图所示,光滑固定斜面C倾角为θ,质量均为m的两物块A、B一起以某一初速沿斜面向上做匀减速直线运动.已知物块A上表面是水平的,则在该减速运动过程中,下列说法正确的是( )| A. | 物块A受到B的摩擦力水平向左 | |
| B. | 物块B受到A的支持力做负功 | |
| C. | 两物块A、B之间的摩擦力大小为mgsinθcosθ | |
| D. | 物块B的机械能减少 |
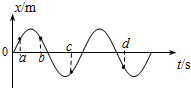
| A. | a时刻质点速度方向沿x轴正方向 | B. | b时刻质点的加速度正在增大 | ||
| C. | c时刻质点的动能正在减小 | D. | d时刻的回复力正在减小 |
 我国的航天事业令世界瞩目.2007年10月、2010年10月20013年12月我国相继成功发射了“嫦娥”一号、“嫦娥”二号、“嫦娥”三号,对月球进行近距离勘察.已知“嫦娥”一号、“嫦娥”二号环绕月球做匀速圆周运动时,距离月球表面高度分别为h1和h2,月球半径为R,月球表面的重力加速度为g.
我国的航天事业令世界瞩目.2007年10月、2010年10月20013年12月我国相继成功发射了“嫦娥”一号、“嫦娥”二号、“嫦娥”三号,对月球进行近距离勘察.已知“嫦娥”一号、“嫦娥”二号环绕月球做匀速圆周运动时,距离月球表面高度分别为h1和h2,月球半径为R,月球表面的重力加速度为g.