题目内容
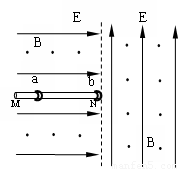
如图所示,在虚线左右两侧均有磁感应强度相同的垂直纸面向外的匀强磁场和场强大小相等方向不同的匀强电场,虚线左侧电场方向水平向右,虚线右侧电场方向竖直向上。左侧电场中有一根足够长的固定绝缘细杆MN,N端位于两电场的交界线上。a、b是两个质量相同的小环(环的半径略大于杆的半径),a环带电,b环不带电,b环套在杆上的N端且处于静止,将a环套在杆上的M端由静止释放,a环先加速后匀速运动到N端,a环与b环在N端碰撞并粘在一起,随即进入右侧场区做半径为 r = 0.10 m的匀速圆周运动,然后两环由虚线上的P点进入左侧场区。已知a环与细杆MN的动摩擦因数μ=0.20,取g = 10 m/s2。求:
1.P点的位置;
2.a环在杆上运动的最大速率。
1.NP = 2r = 0.20 m
2.vmax = 3 m/s
解析:2)NP = 2r = 0.20 m
(2)设电场强度为E,磁感应强度为B,a环的最大速度为Vmin,两环碰后质量为m,电荷量为q。由受力分析可知,a环在杆上速率达到最大时做匀速运动
qE = μFN
qE = μ(mg+qvmaxB)
碰撞时动量守恒 mvmax = 2mv'
碰后两环在右侧场区做匀速圆周运动重力与电场力平衡
qE = 2mg
洛仑兹力提供向心力 q v' B =2m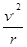
解得: vmax = 3 m/s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
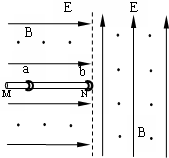 如图所示,在虚线左右两侧均有磁感应强度相同的垂直纸面向外的匀强磁场和场强大小相等方向不同的匀强电场,虚线左侧电场方向水平向右,虚线右侧电场方向竖直向上.左侧电场中有一根足够长的固定绝缘细杆MN,N端位于两电场的交界线上.a、b是两个质量相同的小环(环的半径略大于杆的半径),a环带电,b环不带电,b环套在杆上的N端且处于静止,将a环套在杆上的M端由静止释放,a环先加速后匀速运动到N端,a环与b环在N端碰撞并粘在一起,随即进入右侧场区做半径为 r=0.10m的匀速圆周运动,然后两环由虚线上的P点进入左侧场区.已知a环与细杆MN的动摩擦因数μ=0.20,取g=10m/s2.求:
如图所示,在虚线左右两侧均有磁感应强度相同的垂直纸面向外的匀强磁场和场强大小相等方向不同的匀强电场,虚线左侧电场方向水平向右,虚线右侧电场方向竖直向上.左侧电场中有一根足够长的固定绝缘细杆MN,N端位于两电场的交界线上.a、b是两个质量相同的小环(环的半径略大于杆的半径),a环带电,b环不带电,b环套在杆上的N端且处于静止,将a环套在杆上的M端由静止释放,a环先加速后匀速运动到N端,a环与b环在N端碰撞并粘在一起,随即进入右侧场区做半径为 r=0.10m的匀速圆周运动,然后两环由虚线上的P点进入左侧场区.已知a环与细杆MN的动摩擦因数μ=0.20,取g=10m/s2.求: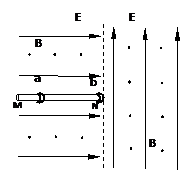 如图所示,在虚线左右两侧均有磁感应强度相同的垂直纸面向外的匀强磁场和场强大小相等方向不同的匀强电场,虚线左侧电场方向水平向右,虚线右侧电场方向竖直向上。左侧电场中有一根足够长的固定绝缘细杆MN,N端位于两电场的交界线上。a、b是两个质量相同的小环(环的半径略大于杆的半径),a环带电,b环不带电,b环套在杆上的N端且处于静止,将a环套在杆上的M端由静止释放,a环先加速后匀速运动到N端,a环与b环在N端碰撞并粘在一起,随即进入右侧场区做半径为 r = 0.10 m的匀速圆周运动,然后两环由虚线上的P点进入左侧场区。已知a环与细杆MN的动摩擦因数μ=0.20,取g = 10 m/s2。求:
如图所示,在虚线左右两侧均有磁感应强度相同的垂直纸面向外的匀强磁场和场强大小相等方向不同的匀强电场,虚线左侧电场方向水平向右,虚线右侧电场方向竖直向上。左侧电场中有一根足够长的固定绝缘细杆MN,N端位于两电场的交界线上。a、b是两个质量相同的小环(环的半径略大于杆的半径),a环带电,b环不带电,b环套在杆上的N端且处于静止,将a环套在杆上的M端由静止释放,a环先加速后匀速运动到N端,a环与b环在N端碰撞并粘在一起,随即进入右侧场区做半径为 r = 0.10 m的匀速圆周运动,然后两环由虚线上的P点进入左侧场区。已知a环与细杆MN的动摩擦因数μ=0.20,取g = 10 m/s2。求: