题目内容
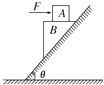
【题目】如图所示,总质量为m的滑雪者以初速度V0沿倾角为θ的斜面向上自由滑行,雪橇与斜面间动摩擦因数为,重力加速度为g,假设斜面足够长.不计空气阻力.试求:
(1)滑雪者沿斜面上滑的加速度大小.
(2)滑雪者沿斜面上滑的最大距离.
(3)若滑雪者滑至最高点后掉转方向向下自由滑行,求沿斜面自由下滑的加速度大小.
【答案】
(1)
解:上滑过程中,对人进行受力分析,滑雪者受重力mg,弹力FN,摩擦力f,并设滑雪者的加速度为a1,受力如图
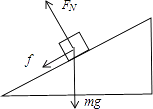
根据牛顿第二定律有:
mgsinθ+f=ma1,①
N=mgcosθ
又f=N
求得:a1=g(sinθ+cosθ)
(2)
解:滑雪者沿斜面向上做匀减速直线运动,则有 v02=2a1x
得 x= ![]()
(3)
解:滑雪者沿斜面向下做匀加速直线运动,受力如图
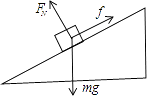
根据牛顿第二定律得 mgsinθ﹣mgcosθ=ma2
求得a2=g(sinθ﹣cosθ)
【解析】(1)滑雪者向上做匀减速直线运动,对其受力分析,求得加速度.(2)由匀变速运动位移公式可以得到上滑的距离.(3)向下自由滑行移做匀加速直线运动,然后受力分析,到加速度.

练习册系列答案
相关题目