题目内容
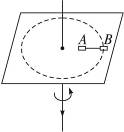
如图5-7-4所示，在水平固定的光滑平板上，有一质量为m的质点P与穿过中央小孔O的轻绳一端相连着，平板与小孔都是光滑的，用手拉着绳子下端，使质点做半径为A、角速度为ω0的匀速圆周运动.若绳子突然放松至某一长度B而立即被拉紧，质点就能在半径为B的圆周上做匀速圆周运动.求质点由半径A到半径B所需的时间及质点在半径为B的圆周上运动的角速度.
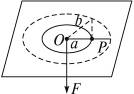
图5-7-4
图5-7-4
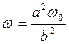.本题考查利用圆周运动、离心运动以及运动的合成和分解等知识综合分析、处理问题的能力.要注意分析质点的运动过程，要明确绳松开后，向心力突然消失，质点沿切线方向飞出，沿光滑平板做匀速直线运动，这是该题的易错点.
质点在半径为A的圆周上以角速度ω0做匀速圆周运动，其线速度为：va=ω0a
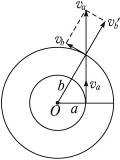
图5-7-5
突然松绳后，向心力消失，质点沿切线方向飞出，以va的速度做匀速直线运动，直到质点m距O点的距离为B时，绳子将被拉直.如图5-7-5所示，作出质点这一过程的俯视图，则质点在匀速直线运动中的位移：
因此质点m由半径A到B所需的时间为：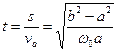
.
当线刚被拉直时，质点的速度为：vA=ω0A
把这一速度分解为垂直于绳的速度vb和沿绳的速度vb′，在绳绷紧的过程中vb′减为零，质点就以vb沿着半径为B的圆周做匀速圆周运动.设其角速度为ω，根据相似三角形得：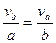
，即
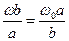，则质点沿半径为B的圆周做匀速圆周运动的角速度为：.
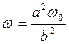质点在半径为A的圆周上以角速度ω0做匀速圆周运动，其线速度为：va=ω0a
图5-7-5
突然松绳后，向心力消失，质点沿切线方向飞出，以va的速度做匀速直线运动，直到质点m距O点的距离为B时，绳子将被拉直.如图5-7-5所示，作出质点这一过程的俯视图，则质点在匀速直线运动中的位移：
因此质点m由半径A到B所需的时间为：
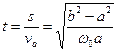.当线刚被拉直时，质点的速度为：vA=ω0A
把这一速度分解为垂直于绳的速度vb和沿绳的速度vb′，在绳绷紧的过程中vb′减为零，质点就以vb沿着半径为B的圆周做匀速圆周运动.设其角速度为ω，根据相似三角形得：
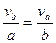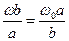，即，则质点沿半径为B的圆周做匀速圆周运动的角速度为：.
练习册系列答案
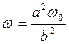名校课堂系列答案
相关题目
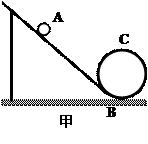
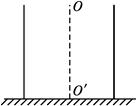
轨道是研究机械能守恒和向心力效果的一套较好的器材（如图甲所示）。某课外研究小组将一个压力传感器安装在轨道最低点B处，他们把一个钢球从轨道上的不同高处由静止释放，得到了多组压力传感器示数F和对应的释放点的高度h，并作出了一个F-h图像（如图乙所示）。根据图中所给信息，回答下列问题（不计各处摩擦）：
时绳对小球的拉力大小；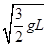
时绳对小球的拉力大小．