Question

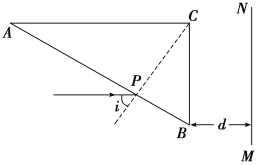
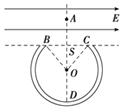
【题目】将一内壁光滑的绝缘细圆管做成的圆环BDC固定在竖直面内，圆环的圆心为O，D为圆环的最低点，其中∠BOC=90°，圆环的半径为R=L，过OD的虚线与过BC的虚线垂直且交于点S，虚线BC的上方存在水平向右的范围足够大的匀强电场。圆心O的正上方A点有一质量为m、带电荷量为-q的绝缘小球（可视为质点），其直径略小于圆管内径，AS=L．现将该小球无初速度释放，经过一段时间小球刚好无碰撞地进入圆管中并继续在圆管中运动，重力加速度大小用g表示。

（1）求虚线BC上方匀强电场的电场强度大小；

（2）求当小球运动到圆环的最低点D时对圆环压力的大小；

（3）小球从管口C离开后，经过一段时间后落到虚线BC上的F点（图中未标出），则C、F两点间的电势差为多大？

Answer 1

【答案】(1) (2) (3)

【解析】

(1)小球在重力和电场力的作用下做匀加速直线运动，从B点沿切线方向进入，则此时速度方向与竖直方向的夹角为45°，即加速度方向与竖直方向的夹角为45°，则场强可求；(2)从A点到D点的过程中，列动能定理表达式，在最低点D时，根据牛顿第二定律列式求解； (3)从A点到B点，根据动能定理求得在B点的速度，从C点抛出后做类平抛运动，抛出时的速度大小与B点速度相当，由运动学公式求出小球沿虚线BC方向运动的位移，再由电势差与场强的关系求解电势差.

(1)小球被释放后在重力和电场力的作用下做匀加速直线运动，小球从B点沿切线方向进入，则此时速度方向与竖直方向的夹角为45°，即加速度方向与竖直方向的夹角为45°，

则:tan45°=

解得:E=

(2)小球从A点到D点的过程中，根据动能定理得mvD2-0=mg(2L+L)+EqL

当小球运动到圆环的最低点D时，根据牛顿第二定律得FN-mg=m

联立解得:FN=3(+1)mg

根据牛顿第三定律得小球运动到圆环的最低点D时对圆环的压力大小为3(+1)mg

(3)小球对A点到B点的过程中，根据动能定理得mvB2-0=mgL+EqL,

解得：vB=2

小球从C点抛出后做类平抛运动，抛出时的速度大小vC=vB=2

小球的加速度大小g′=g

当小球沿抛出方向和垂直抛出方向的位移相等时，回到虚线BC上，则有vCt=g′t2

解得：t=2

则小球沿虚线BC方向运动的位移xCF=vCt=8L

沿着电场线方向电势降低，则C点与F点间的电势差为UCF=-ExCF=-