题目内容
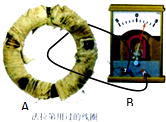
【题目】如图所示,有一固定在水平面的平直轨道,该轨道由白色轨道和黑色轨道交替排列并平滑连接而成.各段轨道的编号已在图中标出.仅黑色轨道处在竖直向上的匀强电场中,一不带电的小滑块A静止在第1段轨道的最左端,绝缘带电小滑块B静止在第1段轨道的最右端.某时刻给小滑块A施加一水平向右的恒力F,使其从静止开始沿轨道向右运动,小滑块A运动到与小滑块B碰撞前瞬间撤去小滑块A所受水平恒力.滑块A、B碰撞时间极短,碰后粘在一起沿轨道向右运动.已知白色轨道和黑色轨道各段的长度均为L=0.10m,匀强电场的电场强度的大小E=1.0×104N/C;滑块A、B的质量均为m=0.010kg,滑块A、B与轨道间的动摩擦因数处处相等,均为μ=0.40,绝缘滑块B所带电荷量q=+1.0×10﹣5C,小滑块A与小滑块B碰撞前瞬间的速度大小v=6.0m/s.A、B均可视为质点(忽略它们的尺寸大小),且不计A、B间的静电力作.在A、B粘在一起沿轨道向右运动过程中电荷量保持不变,取重力加速度g=10m/s2 . 
(1)求F的大小;
(2)碰撞过程中滑块B对滑块A的冲量;
(3)若A和B最终停在轨道上编号为k的一段,求k的数值.
【答案】
(1)
解:以滑块A为研究对象,
在第1段轨道上,滑块A受到摩擦力的大小f=μmg,
对于滑块A在第1段轨道上从最左端到最右端的过程,
根据动能定理得: ![]() ﹣0,
﹣0,
解得:F=1.84N
(2)
解:设滑块A、B碰撞后瞬间A和B的共同速度为vAB,
碰撞过程系统动量守恒,以向右为正方向,
由动量守恒定律得:mv=2mvAB,
设滑块B对滑块A的冲量为I,规定水平向右为正方向.
以滑块A为研究对象,根据动量定理有:I=mvAB﹣mv,
解得:I=﹣0.030Ns,滑块B对滑块A冲量的方向水平向左
(3)
解:设滑块A和B每经过一段长为L的黑色轨道损失的动能为△E1,则△E1=μ(2mg﹣Eq)L,
设滑块A和B每经过一段长为L的白色轨道,损失的动能为△E2,则△E2=μ2mgL,
设滑块A和B碰撞后瞬间的总动能为EkAB,令 ![]() ,解得:N=7.5,
,解得:N=7.5,
即滑块通过标号为15的白色轨道后,仍有动能:Ek=0.5(△E1+△E2)=6×10﹣3J,
因Ek>△E1,故物块可通过第16号轨道而进入第17号轨道,
进入第17号轨道时的动能Ek′=Ek﹣△E1=2×10﹣3J<△E2,
故将不能通过第17号轨道,即最终停在第17号轨道上
【解析】(1)对滑块A应用动能定理可以求出力F的大小;(2)两滑块碰撞过程系统动量守恒,应用动量守恒定律可以求出碰撞后的速度,然后应用动量定理求出B对A的冲量;(3)求出滑块经过黑色与白色轨道时损失的机械能,根据A、B碰撞后的总机械能求出滑块能经过黑白轨道的条数,然后分析求出k的数值.
【考点精析】利用动量定理和动量守恒定律对题目进行判断即可得到答案,需要熟知动量定理的研究对象可以是单个物体,也可以是物体系统.对物体系统,只需分析系统受的外力,不必考虑系统内力.系统内力的作用不改变整个系统的总动量;动量定理不仅适用于恒定的力,也适用于随时间变化的力.对于变力,动量定理中的力F应当理解为变力在作用时间内的平均值;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案