题目内容
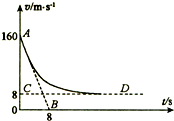“神舟七号”飞船完成了预定空间科学和技术实验任务后，返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回，在离地10km 的高度打开阻力降落伞减速下降，这一过程中若返回舱所受阻力与速度的平方成正比，比例系数（空气阻力系数）为k．设返回舱总质量M=3000kg，所受空气浮力恒定不变，且认为竖直降落．从某时刻开始计时．返回舱的运动v--t图象如图中的AD曲线所示，图中AB是曲线在A点的切线，切线交于横轴一点B的坐标为（8，0），CD是平行横轴的直线，交纵轴于C点，c的坐标为（0，8）．g取10m/s2，请回答下列问题：
（1）在初始时刻v0=160m/s时，它的加速度多大？
（2）推证空气阻力系数的表达式并算出其数值．
（3）返回舱在距离地面高度h=1m时，飞船底部的4个反推力小火箭点 火工作，使其速度由8m/s迅速减至1m/s后落在地面上，若忽略燃料质量的减少对返回舱总质量的影响，并忽略此阶段速度变化而引起空气阻力的变化，试估算每支小火箭的平均推力．（计算结果取两位有效数字）
解：（1）由v-t图象性质可以得，在初始v0=160m/s时，过A点切线的斜率为此时的加速度，设为a1，其大小为：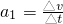
=
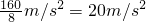
（2）由图知，返回舱的速度变化率逐渐减小，最有是以v1=8m/s的速度做匀速运动，设返回舱受空气浮力为f
在t=0时，由牛顿第二定律：
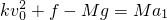
速度为v1=8m/s时，返回舱受力平衡，有
由以上两式解得：
k=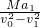
带入数据得：
k=2.35kg/m
（3）设每只小火箭的平均推力为F0，反推加速度为a2，着地速度为v2，由题意知，返回舱在距离地面高度h=1m前，已经处于匀速运动状态，故返回舱在着地前的加速度由4个小火箭的反推力产生，根据牛顿第二定律有：
4F0-Mg=Ma2
又由运动学公式：
由以上两式解得：
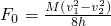
带入数据解得：
F0=24375N
保留两位有效数字得：
F0=2.4×104N
答：
（1）在初始时刻速度为160m/s时，它的加速度为20m/s2
（2）推证空气阻力系数的表达式为k=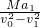，数值k=2.35kg/m
（3）每支小火箭的平均推力为2.4×104N
分析：（1）由v-t图象切线的斜率为此时的加速度，可以得到v0=160m/s时，它的加速度
（2）在v-t图象选取两个点，t=0时，列牛顿第二定律，和v=8m/s时，由于是匀速阶段，故列平衡方程，两式联立可以解得k的表达式和数值
（3）此阶段是在火箭反推力下做的匀减速直线运动，故可以由此求得加速度表达式，再由运动学可以解得推力．
点评：本题的关键点就是对v-t图象的识别和应用，这类题目需要特别注意的是特殊点，即速度和时间都有明确数值的点，另应注意起点，终点，交点，斜率四个知识点．
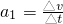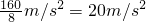
=（2）由图知，返回舱的速度变化率逐渐减小，最有是以v1=8m/s的速度做匀速运动，设返回舱受空气浮力为f
在t=0时，由牛顿第二定律：
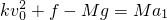
速度为v1=8m/s时，返回舱受力平衡，有
由以上两式解得：
k=
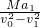
带入数据得：
k=2.35kg/m
（3）设每只小火箭的平均推力为F0，反推加速度为a2，着地速度为v2，由题意知，返回舱在距离地面高度h=1m前，已经处于匀速运动状态，故返回舱在着地前的加速度由4个小火箭的反推力产生，根据牛顿第二定律有：
4F0-Mg=Ma2
又由运动学公式：
由以上两式解得：
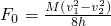
带入数据解得：
F0=24375N
保留两位有效数字得：
F0=2.4×104N
答：
（1）在初始时刻速度为160m/s时，它的加速度为20m/s2
（2）推证空气阻力系数的表达式为k=
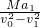，数值k=2.35kg/m（3）每支小火箭的平均推力为2.4×104N
分析：（1）由v-t图象切线的斜率为此时的加速度，可以得到v0=160m/s时，它的加速度
（2）在v-t图象选取两个点，t=0时，列牛顿第二定律，和v=8m/s时，由于是匀速阶段，故列平衡方程，两式联立可以解得k的表达式和数值
（3）此阶段是在火箭反推力下做的匀减速直线运动，故可以由此求得加速度表达式，再由运动学可以解得推力．
点评：本题的关键点就是对v-t图象的识别和应用，这类题目需要特别注意的是特殊点，即速度和时间都有明确数值的点，另应注意起点，终点，交点，斜率四个知识点．
练习册系列答案
相关题目
2008年9月25日21时10分，神舟七号飞船成功发射，共飞行2天20小时27分钟，绕地球飞行45圈后，于9月28日17时37分安全着陆．航天员翟志刚着“飞天”舱外航天服，在刘伯明的配合下，成功完成了空间出舱活动，进行了太空行走．出舱活动结束后，释放了伴飞卫星，并围绕轨道舱进行伴飞实验．神舟七号是由长征-2F运载火箭将其送入近地点为A，远地点为B的椭圆轨道上，实施变轨后，进入预定圆轨道，其简化的模拟轨道如图12所示．假设近地点A距地面高度为h，飞船在预定圆轨道上飞行n圈所用的时间为t，地球表面的重力加速度为g，地球半径R，试求：
“神舟七号”飞船完成了预定空间科学和技术实验任务后，返回舱于2008年9月28日17时37分开始从太空向地球表面按预定轨道返回，在离地10km 的高度打开阻力降落伞减速下降，这一过程中若返回舱所受阻力与速度的平方成正比，比例系数（空气阻力系数）为k．设返回舱总质量M=3000kg，所受空气浮力恒定不变，且认为竖直降落．从某时刻开始计时．返回舱的运动v--t图象如图中的AD曲线所示，图中AB是曲线在A点的切线，切线交于横轴一点B的坐标为（8，0），CD是平行横轴的直线，交纵轴于C点，c的坐标为（0，8）．g取10m/s2，请回答下列问题：