题目内容
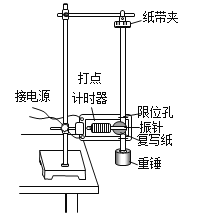
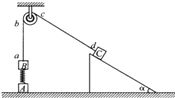
【题目】如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上,B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的足够长的光滑斜面上,用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细绳竖直,cd段的细绳与斜面平行,已知A、B的质量均为m,C的质量为M(M>2m),重力加速度为g,细绳与滑轮之间的摩擦不计,开始时整个系统处于静止状态,释放C后它沿斜面下滑,当A刚离开地面时,B获得最大速度(B未触及滑轮,弹簧始终处于弹性限度内),求:
(1)从释放C弹簧的压缩量;
(2)物体B的最大速度vm;
(3)若C与斜面间动摩擦因数为μ,从释放C开始到物体A恰好要离开地面时,细线对物体C所做的功。
【答案】(1)![]() (2)
(2)![]()
(3)![]()
【解析】试题分析:据题意:释放物体C之前细线恰好伸直但没有拉力,弹簧所受的压力等于a的重力,根据胡克定律求解弹簧的压缩量x;当A恰好要离开地面时,地面对物体A的支持力为零,根据胡克定律求出此时弹簧的伸长量x′,则物体B上升的高度和物体C沿斜面下滑的距离等于x+x′.当物体B达最大速度时合力为零,根据平衡条件和三个物体和弹簧的机械能守恒,列式可求解物体B的最大速度.以三个物体和弹簧作为研究对象,据动能定理求出物体A恰好要离开地面时B、C的速度大小,再对C,运用动能定理求解细线对物体C所做的功
细线恰好伸直,绳子拉力为零,设弹簧的压缩量为x
对B受力分析有:mg=kx, 解得:![]()
(2)当A恰好要离开地面时,地面对物体A的支持力为零,设弹簧的伸长量为x′
对物体A受力分析有:![]()
C下滑的距离为:![]()
设斜面倾角为α
当物体B达最大速度时有:Mgsinα=2mg
根据动能定理得:Mgssinα-mgs=![]()
解得:![]()
(3)以三个物体和弹簧作为研究对象,据动能定理有:
![]()
以物体C为研究对象,据动能定理有:
![]()
解得:![]()