Question

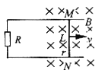
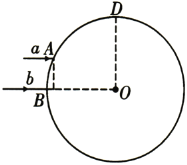
【题目】如图所示，一圆形磁场区域半径为R，有垂直于纸面向里的匀强磁场，有a、b两个完全相同的粒子（重力忽略）以相同速度水平向右分别从A、B两点射入圆形磁场区域（从B点射入的粒子速度沿半径方向），其中从B点射入的粒子刚好从圆形磁场的最上端D点离开，A点离BO的距离为，则a、b两个粒子在磁场中运动的时间：之比为

A. 1:2 B. : C. 2：3 D. 1：

Answer 1

【答案】C

【解析】

根据要求画出粒子的运动轨迹，确定两个粒子在磁场中运动的圆心角，利用周期相等，根据求出时间之比。

由题可知，两个粒子在磁场中运动的半径相同，由于从B点射入的粒子刚好从圆形磁场的最上端D点离开，可知两个粒子的半径都为R，如图所示：

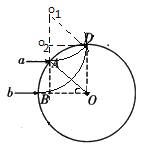
由几何关系可知，从A点入射的粒子在磁场中运动的圆心角为，从B点入射的粒子在磁场中运动的圆心角为，根据运动时间，得a、b两个粒子在磁场中运动的时间，故选C。