题目内容
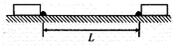
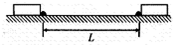为了限制汽车的速度，某些路段需要设置“减速墩”（路面上凸起的条状装置）．某平直路段相隔L=20m设立了两个减速墩，如图11所示．汽车通过每个减速墩时允许的最大速度为ν0=2m/s，汽车加速时的最大加速度大小为a1=3m/s2，减速时的最大加速度大小为a2=6m/s2．，汽车长度为d=5m，设汽车过每个减速墩时均保持匀速行驶，减速墩宽度不计，求汽车通过这两个减速墩所需的最短时间．分析：当汽车匀速通过减速墩，在两个减速墩之间先加速再减速运动时，所用的时间最短，抓住匀加速直线运动和匀减速直线运动的位移之和，通过运动学公式求出最短的时间．
解答：解：车匀速通过两个减速墩的时间t1=
=5s．
车先加速后减速通过两个减速墩之间的位移x=L-d=15m
设最大速度为v，则v2-v02=2a1x1
v2-v02=2a2x2
x=x1+x2=
+
解得v=8m/s．
汽车通这一路段所需的最短时间t=t1+
+
=8s．
答：汽车通过这两个减速墩所需的最短时间为8s．
| 2d |
| v0 |
车先加速后减速通过两个减速墩之间的位移x=L-d=15m
设最大速度为v，则v2-v02=2a1x1
v2-v02=2a2x2
x=x1+x2=
| v2-v02 |
| 2a1 |
| v2-v02 |
| 2a2 |
解得v=8m/s．
汽车通这一路段所需的最短时间t=t1+
| v-v0 |
| a1 |
| v-v0 |
| a2 |
答：汽车通过这两个减速墩所需的最短时间为8s．
点评：解决本题的关键理清汽车的运动情况，结合运动学公式灵活求解．
练习册系列答案
相关题目
时，车对桥顶的压力为车重的
，为了安全起见，汽车不能飞离桥面，汽车在桥顶时的速度应限制在 m/s内。 
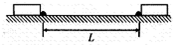为了限制汽车的速度，某些路段需要设置“减速墩”（路面上凸起的条状装置）．某平直路段相隔L=20m设立了两个减速墩，如图11所示．汽车通过每个减速墩时允许的最大速度为ν0=2m/s，汽车加速时的最大加速度大小为a1=3m/s2，减速时的最大加速度大小为a2=6m/s2．，汽车长度为d=5m，设汽车过每个减速墩时均保持匀速行驶，减速墩宽度不计，求汽车通过这两个减速墩所需的最短时间．