题目内容
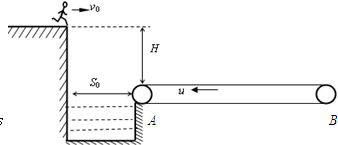 (2012?浠水县模拟)参加电视台娱乐节目,选手要从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=1.0s反应时间后,立刻以a=2m/s2恒定向右加速度跑至传送带最右端.
(2012?浠水县模拟)参加电视台娱乐节目,选手要从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=1.0s反应时间后,立刻以a=2m/s2恒定向右加速度跑至传送带最右端.(1)若传送带静止,选手以v0=3m/s水平速度从平台跃出,求从开始跃出到跑至传送带右端经历的时间.
(2)若传送带以u=1m/s的恒定速度向左运动,选手要能到达传送带右端,他从高台上跃出的水平速度v1至少多大?在此情况下到达B点时刻速度大小是多少?
分析:(1)从开始跃出到跑至传送带右端经历的时间经历两个过程:平抛运动和匀加速直线运动.平抛运动的时间可以通过竖直方向去求,因为平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,求出水平位移,然后再求出匀加速运动的位移以及时间.
(2)选手平抛运动到传送带上后,在反应时间内跟传送带一起向左做匀速,然后以2m/s2的加速度向左做匀减速直线运动到0,如果在这段时间内未掉入水中,则不会调入水中,以后向右做初速度为0的匀加速直线运动.
(2)选手平抛运动到传送带上后,在反应时间内跟传送带一起向左做匀速,然后以2m/s2的加速度向左做匀减速直线运动到0,如果在这段时间内未掉入水中,则不会调入水中,以后向右做初速度为0的匀加速直线运动.
解答:解:(1)H=
gt12,t1=
=0.6s
选手在水平方向上的位移s1=v0t1=1.8m
则匀加速运动的位移s2=L0+s0-s1=
at22 t2=4.4s t=t1+t2+△t=6.0s
(2)设水平跃出速度v1,落到传送带1s反应时间内向左位移大小s1=u△t=1m
然后向左减速至速度为零,向左发生位移 s2=
=0.25m
不从传送带上掉下,平抛水平位移 s≥S0+s1+s2=2.45m
则 v1≥
=4.08m/s 最小速度为4.08m/s
在此情况下到达B点时刻速度v2=2aL0
v=
=
m/s.
故本题答案为:6.0s,
m/s.
| 1 |
| 2 |
|
选手在水平方向上的位移s1=v0t1=1.8m
则匀加速运动的位移s2=L0+s0-s1=
| 1 |
| 2 |
(2)设水平跃出速度v1,落到传送带1s反应时间内向左位移大小s1=u△t=1m
然后向左减速至速度为零,向左发生位移 s2=
| u2 |
| 2a |
不从传送带上掉下,平抛水平位移 s≥S0+s1+s2=2.45m
则 v1≥
| s |
| t1 |
在此情况下到达B点时刻速度v2=2aL0
v=
| 2aL0 |
| 80 |
故本题答案为:6.0s,
| 80 |
点评:解决本题的关键分析出选手的运动情况,然后根据平抛运动和运动学公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?浠水县模拟)在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高).则绳中拉力大小变化的情况是( )
(2012?浠水县模拟)在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高).则绳中拉力大小变化的情况是( )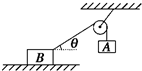 (2012?浠水县模拟)如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为mA、mB,绳与水平方向的夹角为θ,则( )
(2012?浠水县模拟)如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为mA、mB,绳与水平方向的夹角为θ,则( )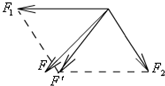 (2012?浠水县模拟)在验证力的平行四边形定则的实验中,根据实验数据画出力的图示(如图所示).图上标出了F1、F2、F、F'四个力,其中不是由弹簧秤直接测得的力是
(2012?浠水县模拟)在验证力的平行四边形定则的实验中,根据实验数据画出力的图示(如图所示).图上标出了F1、F2、F、F'四个力,其中不是由弹簧秤直接测得的力是