题目内容
（2012?浠水县模拟）在上海世博会最佳实践区，江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色．如图所示，在竖直放置的穹形光滑支架上，一根不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G．现将轻绳的一端固定于支架上的A点，另一端从B点沿支架缓慢地向C点靠近（C点与A点等高）．则绳中拉力大小变化的情况是（ ）分析：当轻绳的右端从B点移到直杆最上端时，两绳的夹角增大．滑轮两侧绳子的拉力大小相等，方向关于竖直方向对称．以滑轮为研究对象，根据平衡条件研究绳的拉力变化情况．当轻绳的右端从直杆的最上端移到C点的过程中，根据几何知识分析得到滑轮两侧绳子的夹角不变，由平衡条件判断出绳子的拉力保持不变．
解答：解：
当轻绳的右端从B点移到直杆最上端时，设两绳的夹角为2θ．以滑轮为研究对象，分析受力情况，作出力图如图1所示．根据平衡条件得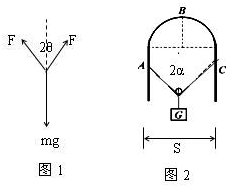
2Fcosθ=mg
得到绳子的拉力F=
所以在轻绳的右端从B点移到直杆最上端时的过程中，θ增大，cosθ减小，则F变大．
当轻绳的右端从直杆最上端移到C点时，设两绳的夹角为2α．
设绳子总长为L，两直杆间的距离为S，由数学知识得到
sinα=
，L、S不变，则α保持不变．
再根据平衡条件可知，两绳的拉力F保持不变．
所以绳中拉力大小变化的情况是先变大后不变．
故选C
当轻绳的右端从B点移到直杆最上端时，设两绳的夹角为2θ．以滑轮为研究对象，分析受力情况，作出力图如图1所示．根据平衡条件得
2Fcosθ=mg
得到绳子的拉力F=
| mg |
| 2cosθ |
所以在轻绳的右端从B点移到直杆最上端时的过程中，θ增大，cosθ减小，则F变大．
当轻绳的右端从直杆最上端移到C点时，设两绳的夹角为2α．
设绳子总长为L，两直杆间的距离为S，由数学知识得到
sinα=
| S |
| L |
再根据平衡条件可知，两绳的拉力F保持不变．
所以绳中拉力大小变化的情况是先变大后不变．
故选C
点评：本题是共点力平衡中动态变化分析问题，关键在于运用几何知识分析α的变化，这在高考中曾经出现过，有一定的难度．
练习册系列答案
相关题目
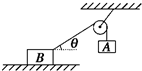（2012?浠水县模拟）如图所示，轻质光滑滑轮两侧用细绳连着两个物体A与B，物体B放在水平地面上，A、B均静止．已知A和B的质量分别为mA、mB，绳与水平方向的夹角为θ，则（ ）
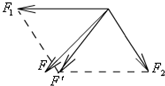（2012?浠水县模拟）在验证力的平行四边形定则的实验中，根据实验数据画出力的图示（如图所示）．图上标出了F1、F2、F、F'四个力，其中不是由弹簧秤直接测得的力是