题目内容
在水平足够长的固定木板上，一小物块以某一初速度开始滑动，经一段时间t后停止，现将该木板改置成倾角为θ的斜面，让小物块以相同的初速度沿木板上滑，若小物块上滑到最高位置所需时间也为t，则小物块与木板之间的动摩擦因数μ为（ ）
分析：当物块在水平面上滑动时，合力为摩擦力，根据牛顿第二定律得出加速度．在斜面上滑动，根据牛顿第二定律也得出加速度．然后根据运动学公式，抓住时间相等，求出μ．
解答：解：物块在水平面上滑行时加速度a1=
=μg，在倾角为θ的斜面上上滑时加速度a2=
=gsinθ+μgcosθ
根据初速度和时间相等，即
=
知a1=a2，即μg=gsinθ+μgcosθ
则μ=
，故B正确，A、C、D错误．
故选B．
| μmg |
| m |
| mgsinθ+μmgcosθ |
| m |
根据初速度和时间相等，即
| v0 |
| a1 |
| v0 |
| a2 |
知a1=a2，即μg=gsinθ+μgcosθ
则μ=
| sinθ |
| 1-cosθ |
故选B．
点评：解决本题的关键根据牛顿第二定律求出加速度，再根据匀变速直线运动速度时间公式进行分析．
练习册系列答案
阅读快车系列答案
相关题目
（2013?德州二模）如图所示，AB段为一半径R=0.2m的光滑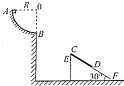
圆弧轨道，EF为一倾角是30°的足够长的光滑固定斜面，斜而上有一质量为0.1kg的薄木板CD，开始时薄木板被锁定．一质量也为0.1kg的物块从且点由静止开始下滑，通过B点后水平抛出，经过一段时间后恰好以平行于薄木板的方向滑上薄木板，在物块滑上薄木板的同时薄木饭，解除锁定，下滑过程中某时刻物块和薄木板能达到共同速度．已知物块与薄木板间的动摩擦因数为
．（g=10m/s2，结果可保留根号）求：
的斜面，让小物块以相同的初速度沿木反上滑。若小物块与木板之间的动摩擦因数为
，则小物块上滑到最高位置所需时间与t之比为
B．
C．
D．
的斜面，让小物块以相同的初速度沿木反上滑。若小物块与木板之间的动摩擦因数为
，则小物块上滑到最高位置所需时间与t之比为
B．
C．
D．