题目内容
有一长度为l = 1m的木块A，放在足够长的水平地面上。取一无盖长方形木盒B将A罩住，B的左右内壁间的距离为L = 3m。A、B质量相同，与地面间的动摩擦因数分别为uA= 0.1和uB = 0.2。开始时A与B的左内壁接触，两者以相同的初速度v0 =18m/s向右运动。已知A与B的左右内壁发生的碰撞时间极短，且不存在机械能损失，A与B的其它侧面无接触。求：⑴开始运动后经过多长时间A、B发生第一次碰撞；
⑵第一次碰撞碰后的速度vA和vB；
⑶通过计算判断A、B最后能否同时停止运动？若能，则经过多长时间停止运动？若不能，哪一个先停止运动？
⑷若仅v0未知，其余条件保持不变，要使A、B最后同时停止，而且A与B轻轻接触（即无相互作用力），则初速度v0应满足何条件？（只需给出结论，不要求写出推理过程）
⑴木块和木盒分别做匀减速运动，加速度大小分别为：aA = μAg = 1m/s2 aB = μBg = 2m/s2 设经过时间T发生第一次碰撞 则有：L－l = SA－SB = V0T－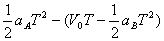
代入数据得：T = 2s ⑵碰前木块和木盒的速度分别为：VA′=V0-aAT=16m/s VB′=V0-aBT=14m/s相碰过程动量守恒有：mvA′+mvB′= mvA+mvB 
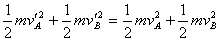代入数据得： vA=vB′=14m/s 方向向右 vB = vA′=16m/s 方向向右 ⑶设第一次碰撞后又经过T1时间，两者在左端相遇有： L－l = SB－SA SB= vB T1－
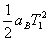SA= vA T1－
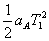代入数据得；T1=T=2s 在左端相碰前：木块、木盒速度分别为：
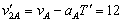m/s 
m/s 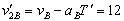可见木块、木盒经过时间t1=2T在左端相遇接触时速度恰好相同 同理可得：木块、木盒经过同样时间t2 = 2T，第二次在左端相遇 
m/s木块、木盒第三次又经过同样时间t3=2T在左端相遇，速度恰好为零。由上可知：木块、木盒，最后能同时停止运动 经历的时间：t总= 6T = 12s (4)由⑵归纳可知：v0 = 6K(K取：1，2，3)
代入数据得：T = 2s ⑵碰前木块和木盒的速度分别为：VA′=V0-aAT=16m/s VB′=V0-aBT=14m/s相碰过程动量守恒有：mvA′+mvB′= mvA+mvB 代入数据得： vA=vB′=14m/s 方向向右 vB = vA′=16m/s 方向向右 ⑶设第一次碰撞后又经过T1时间，两者在左端相遇有： L－l = SB－SA SB= vB T1－ SA= vA T1－ 代入数据得；T1=T=2s 在左端相碰前：木块、木盒速度分别为：m/s m/s 可见木块、木盒经过时间t1=2T在左端相遇接触时速度恰好相同 同理可得：木块、木盒经过同样时间t2 = 2T，第二次在左端相遇 m/s木块、木盒第三次又经过同样时间t3=2T在左端相遇，速度恰好为零。由上可知：木块、木盒，最后能同时停止运动 经历的时间：t总= 6T = 12s (4)由⑵归纳可知：v0 = 6K(K取：1，2，3) 
练习册系列答案
相关题目
在水平长直的轨道上，有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动．某时刻将一质量为m的小滑块轻放到车面的中点，滑块与车面间的动摩擦因数为μ=0.2，滑块质量m=1kg，车长=2m，车速v0=4m/s，取g=10m/s2，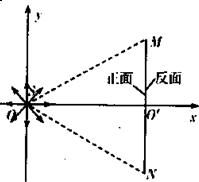
如图所示，在直角坐标系xOy的原点O处有一放射源S，放射源S在xOy平面内均匀发射速度大小相等的正电粒子，位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN，荧光屏正反两侧均涂有荧光粉，MN与x轴交于O'点．已知三角形MNO为正三角形，放射源S射出的粒子质量为m，带电荷量为q，速度大小为v，不计粒子的重力．
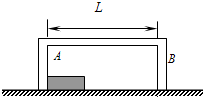有一长度为l=1m的木块A，放在足够长的水平地面上．取一无盖长方形木盒B将A罩住，B的左右内壁间的距离为L=3m．A、B质量相同，与地面间的动摩擦因数分别为uA=0.1和uB=0.2．开始时A与B的左内壁接触，两者以相同的初速度v0=18m/s向右运动．已知A与B的左右内壁发生的碰撞时间极短，且不存在机械能损失，A与B的其它侧面无接触．求：
如图所示，在水平长直的轨道上，有一长度为L的平板车在外力控制下始终保持速度v0，做匀速直线运动．某时刻将一质量为m，可视为质点的小滑块轻放到车面距右端