题目内容
3．
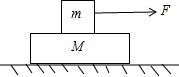如图所示，质量为M的长木板位于光滑水平面上，质量为m的物块静止在长木块上，两物块之间的滑动摩擦因数为μ，现对物块m施加水平向右的恒力F，若恒力F使长木板与物块出现相对滑动．则恒力F的最小值为（重力加速度大小为g，物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力）（ ）| A． | μmg（1+$\frac{m}{M}$） | B． | μmg（1+$\frac{M}{m}$） | C． | μmg | D． | μMg |
分析 当AB相对滑动，F的最小值为A、B间的能达到的最大静摩擦力．根据牛顿第二定律求出F的最小值．
解答 解：对m、M整体进行受力分析：F=（M+m）a
对m进行受力分析：F-fB=ma
对M进行受力分析：fA=Ma
当m、M即将相对滑动时，静摩擦力达到最大值，fA=μmg．求解上面方程组，
F最小=μmg（1+$\frac{m}{M}$），故A正确、BCD错误．
故选：A．
点评 解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，注意临界状态和整体法、隔离法的运用．
练习册系列答案
相关题目
11．
如图所示水平圆半径为R，两直径AB和CD垂直，A、B、C、D四点处各分布着四个带电量均为q的正电荷，O为圆心，OP是过圆心的竖直直线．把一个带电量也为q的带正电的小球（看作点电荷）放在直线OP上的Q点，小球刚好能静止，Q点到圆心O的距离为$\sqrt{3}$R．现把此小球从Q点上方的E点静止释放，小球能运动到Q点下方的最低点F（E、F点位画出）．已知E、F两点间的距离为h，静电常数为k，重力加速度为g．则（ ）
如图所示水平圆半径为R，两直径AB和CD垂直，A、B、C、D四点处各分布着四个带电量均为q的正电荷，O为圆心，OP是过圆心的竖直直线．把一个带电量也为q的带正电的小球（看作点电荷）放在直线OP上的Q点，小球刚好能静止，Q点到圆心O的距离为$\sqrt{3}$R．现把此小球从Q点上方的E点静止释放，小球能运动到Q点下方的最低点F（E、F点位画出）．已知E、F两点间的距离为h，静电常数为k，重力加速度为g．则（ ）| A． | 小球的质量是$\frac{\sqrt{3}k{q}^{2}}{{R}^{2}g}$ | |
| B． | 直线OP上场强最大的位置一定在F点的下方 | |
| C． | 直线OP上沿O点到P点电势逐渐升高 | |
| D． | E、F两点间的电势差为UEF=-$\frac{\sqrt{3}kqh}{2{R}^{2}}$ |
18．下列说法正确的是（ ）
| A． | 光电效应发生时减小入射光的强度，光电子的最大初动能不变 | |
| B． | 氢原子从高能级跃迁到低能级，氢原子核外的电子的动能增大，电势能减小，吸收光子 | |
| C． | 将放射性元素掺杂到其它稳定元素中，并降低其温度，该元素的半衰期将增大 | |
| D． | ${\;}_{92}^{238}$U（轴核）要衰变成${\;}_{86}^{222}$Rn（氡核）需要发生4次α衰变和2次β衰变 | |
| E． | 核子结合成原子核时质量减小 |
8．已知方向不定的三个力的大小分别为F1=4N、F2=5N、F3=6N．则这三个力的合力的最小值为（ ）
| A． | 0 | B． | 1N | C． | 2N | D． | 3N |
15．
如图所示，倾角为30°的斜面上，质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$（g为重力加速度）向上加速运动距离x的过程中，下列说法正确的（ ）
如图所示，倾角为30°的斜面上，质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$（g为重力加速度）向上加速运动距离x的过程中，下列说法正确的（ ）| A． | 重力势能增加mgs | B． | 动能增加$\frac{1}{4}$mgs | C． | 机械能增加mgs | D． | 拉力做功为$\frac{1}{2}$mgs |
12．有a、b两个粒子，质量之比是ma：mb=1：2，带电量之比是qa：qb=2：1，将a、b两个粒子从静止开始经过同一电场（ ）
| A． | 加速后a粒子的速度较大 | |
| B． | 在电场中同一点b粒子受到的电场力较大 | |
| C． | 加速后a粒子的动能较小 | |
| D． | 在电场中同一点b粒子的加速度较大 |