��Ŀ����
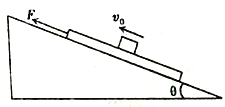
����Ŀ����ͼ��ʾ��һ�㹻��б�������=37����б������һ����Ϊm=1kg��ľ�壬��ľ���Ϸ�һ����ҲΪm=1kg�Ľ����飨�ɿ����ʵ㣩��t=0ʱ�̽�������ٶ�Ϊv0=20m/s��������б�����ϣ�ͬʱ��ľ��ʩ��һ����б�����ϵ�����F=14N��ʹľ��Ӿ�ֹ��ʼ�˶�����t=2sʱ��ȥ����F����֪�������ľ��䶯Ħ��������1=0.25��ľ���б��䶯Ħ��������2=0.5��![]() ���������ٶ�
���������ٶ�![]() �����Ħ�������ڻ���Ħ��������
�����Ħ�������ڻ���Ħ��������
��1��ǰ2s�ڽ������ľ��ļ��ٶ���
��2����t=0���������ٶȼ�С��0�Ĺ�����ľ����б���ϵ�λ�ƣ��˹��̽�����ʼ��δ�뿪ľ�壬������������λ��Ч���֣���
���𰸡���1��![]() ��
��![]() ��2��
��2��![]()
��������(1)�Խ������ľ��Ӧ��ţ���˶�������![]()
![]()
��ý�����ļ��ٶ�![]() ��������б�����£�
��������б�����£�
ľ��ļ��ٶ�![]() ��������б��������
���������������
(3)2sĩ��������ٶ�Ϊ![]() ��
��
ľ����ٶ�Ϊ![]()
�ɼ���ȥFʱ�������ľ���ٶ���ȡ�
������֪�˺�һ��ʱ�������ļ��ٶ���Ϊ![]() ��������б�����¡�
��������б�����¡�
��˺�һ��ʱ���ļ��ٶ�Ϊ![]() ��
��
��ţ�ٵڶ����ɿɵ���![]() ��
��
���![]() ��������б�����¡�
��������б�����¡�
����![]() ����ľ���ٶ��ȼ����㣬�˺��ڽ������ϻ��Ĺ����У�����ľ�徲ֹ��б����б���ϣ��ܵ�б��ľ�Ħ����Ϊf����
����ľ���ٶ��ȼ����㣬�˺��ڽ������ϻ��Ĺ����У�����ľ�徲ֹ��б����б���ϣ��ܵ�б��ľ�Ħ����Ϊf����![]() ��f=4N
��f=4N
ľ���б��֮������Ħ����![]() ,
,![]() �����������
�����������
��������ٶȼ�С��0,�Ĺ�����ľ����б���ϻ�����λ��Ϊx����![]() ��������б��������
���������������