题目内容
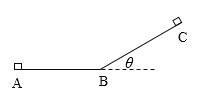
【题目】如图所示，一质量为m小物体，在大小为F的水平恒力作用下，从光滑水平面上的A点由静止出发，运动到倾角为θ的光滑斜面后做减速运动到C点，水平面和斜面在B点平滑连接。
（1）求小物体在斜面上运动时所受的支持力N和加速度a的大小
（2）若水平面AB和斜面BC长均为s，则从A到C的过程中恒力F做的总功为多少？
【答案】（1）a =gsinθ – Fcosθ/m（2）Fs+Fscosθ
【解析】（1）小物体在斜面上的受力分析如图所示
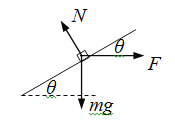
物体沿斜面方向减速上升，合力沿斜面向下，由牛顿定律得
mgsinθ – Fcosθ=ma
物体在垂直于斜面方向平衡，合力为0，有
N= Fsinθ + mgcosθ
由上述两式得：a =gsinθ – Fcosθ/m
（2）物体在水平面上运动时，恒力F方向与位移方向夹角为0
恒力做功为W1= Fs
物体在斜面上运动时，恒力F方向与位移方向夹角为θ
恒力做功为W2= Fscosθ
由于功为标量，恒力做的总功W=W1+W2=Fs+Fscosθ
练习册系列答案
相关题目
