题目内容
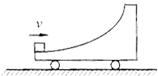 如图所示,一辆光滑曲面小车,静止在光滑水平面上,一木块以一定的速度开始沿小车曲面上滑,小车的质量为木块质量的4倍,当小车被固定时,木块沿曲面上滑的最大高度为h,求:
如图所示,一辆光滑曲面小车,静止在光滑水平面上,一木块以一定的速度开始沿小车曲面上滑,小车的质量为木块质量的4倍,当小车被固定时,木块沿曲面上滑的最大高度为h,求:(1)小木块的初速度为多大?
(2)若小车不被固定,则木块沿曲面可上滑的最大高度为多大?
分析:(1)当小车被固定时,木块沿曲面上滑过程,只有重力做功,机械能守恒,即可根据机械能守恒定律列式求出木块的初速度.
(2)若小车不被固定时,木块上滑过程中小车向右运动,两者组成的系统水平方向不受外力,系统水平方向的动量守恒,同时遵守机械能守恒,根据两大守恒列式求解.
(2)若小车不被固定时,木块上滑过程中小车向右运动,两者组成的系统水平方向不受外力,系统水平方向的动量守恒,同时遵守机械能守恒,根据两大守恒列式求解.
解答:解:(1)设木块的质量为m,小车的质量为4m.
当小车被固定时,木块沿曲面上滑过程,只有重力做功,机械能守恒,则得:
mgh=
m
①
则得,小木块的初速度为 v0=
.②
(2)若小车不被固定,设木块滑到最大高度时小车与木块的共同速度为v,最大高度为H.
木块上滑过程中小车向右运动,两者组成的系统水平方向不受外力,系统水平方向的动量守恒,则得:
mv0=(m+4m)v ③
又系统的机械能守恒,则得:
m
=
(m+4m)v2+mgH ④
联立②③④解得,H=
h.
答:
(1)小木块的初速度为
.
(2)若小车不被固定,则木块沿曲面可上滑的最大高度为
h.
当小车被固定时,木块沿曲面上滑过程,只有重力做功,机械能守恒,则得:
mgh=
| 1 |
| 2 |
| v | 2 0 |
则得,小木块的初速度为 v0=
| 2gh |
(2)若小车不被固定,设木块滑到最大高度时小车与木块的共同速度为v,最大高度为H.
木块上滑过程中小车向右运动,两者组成的系统水平方向不受外力,系统水平方向的动量守恒,则得:
mv0=(m+4m)v ③
又系统的机械能守恒,则得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
联立②③④解得,H=
| 4 |
| 5 |
答:
(1)小木块的初速度为
| 2gh |
(2)若小车不被固定,则木块沿曲面可上滑的最大高度为
| 4 |
| 5 |
点评:本题第2小题是两个物体相互作用问题,优先考虑系统的动量和机械能是否守恒,要准确选择物理规律进行分析和求解.

练习册系列答案
相关题目
