题目内容
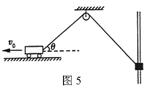
在抗洪抢险中，战士驾驶冲锋舟救人，假设江岸是平直的，洪水沿江而下，水的流速为5m/s，舟在静水中的航速为l0m/s，战士救人的地点A离岸边最近点0的距离为50m如图，问：
(1)战士要想通过最短的时间将人送上岸，求最短时间为多长?
(2)战士要想通过最短的航程将人送上岸，冲锋舟的驾驶员应将舟头与河岸成多少度角开?
(3)如果水的流速是10m/s，而舟的航速(静水中)为5m/s，战士想通过最短的距离将人送上岸，求这个最短的距离．
(1)战士要想通过最短的时间将人送上岸，求最短时间为多长?
(2)战士要想通过最短的航程将人送上岸，冲锋舟的驾驶员应将舟头与河岸成多少度角开?
(3)如果水的流速是10m/s，而舟的航速(静水中)为5m/s，战士想通过最短的距离将人送上岸，求这个最短的距离．
(1) t="5s " (2) θ=600 (3) s=100m
(1)根据运动的独立性可知，冲锋舟到达江岸的时间是由垂直于江岸的分速度决定，该分速度越大，则时间越短，故当冲锋舟垂直于江岸时，时间最短，设船在静水中的速度为v2,水速为v1,最短的时间为t=d/v2=5s
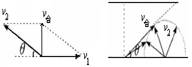
(2)战士要想到达江岸的过程中航程最短，则要求合速度的方向垂直于江岸，舟头必须斜向上，设与江岸的夹角为θ (如图2所示)，则cosθ=v1/v2=0.5，θ=600
(3)在v1>v2的条件下，舟只能斜向下游到江岸，此时v2所有可能的方向如图所示，v合与v2垂直时θ角最大，位移最短，此时sinθ=v2/v1=0.5，则θ=300，最短位移为s=50/sin300=100m
(2)战士要想到达江岸的过程中航程最短，则要求合速度的方向垂直于江岸，舟头必须斜向上，设与江岸的夹角为θ (如图2所示)，则cosθ=v1/v2=0.5，θ=600
(3)在v1>v2的条件下，舟只能斜向下游到江岸，此时v2所有可能的方向如图所示，v合与v2垂直时θ角最大，位移最短，此时sinθ=v2/v1=0.5，则θ=300，最短位移为s=50/sin300=100m
练习册系列答案
相关题目
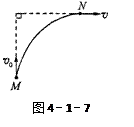
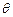，此时小车的速度为
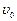，则此时货物的速度为
