题目内容
如图所示,在匀强磁场中竖直放置两条足够长的平行导轨,磁场方向与导轨所在平面垂直,磁感强度大小为B0。导轨上端连接一阻值为R的电阻和电键K,导轨电阻不计。两金属棒a和b的电阻都为R,质量分别为ma=0.02kg和mb=0.01kg,它们与导轨接触良好,并可沿导轨无摩擦地运动,g取10m/s2。

(1)若将b棒固定,电键K断开,用一竖直向上的恒力F拉a棒,稳定后a棒以v1=10m/s的速度向上匀速运动。此时再释放b棒,b棒恰能保持静止。求拉力F的大小。
(2)若将a棒固定,电键K闭合,让b棒自由下滑,求b棒滑行的最大速度v2。
(3)若将a棒和b棒都固定,电键K断开,使磁感强度从B0随时间均匀增加,经0.1s后磁感强度增大到2B0时a棒所受到的安培力大小正好等于a棒的重力,求两棒间的距离h。
(1)0.3N (2)7.5m/s (3)1.0m
【解析】
试题分析:(20分,第1小问4分,第2小问8分,第3小问8分)
解:(1)a棒作切割磁感线运动,产生感应电动势,有:
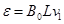 (1)
1分
(1)
1分
a棒与b棒构成串联闭合电路,电流强度为
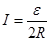 (2)
1分
(2)
1分
a棒、b棒受到的安培力大小为
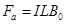 (3)
(3)
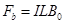 (4)
1分
(4)
1分
依题意,有 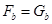 (5)
(5)
解得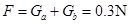 1分
1分
[注:将a、b棒看作整体,安培力看作内力,直接得到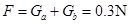 同样给4分。](2)a棒固定、电键K闭合后,b棒自由下滑作切割磁感线运动,最终b棒以最大速度v2匀速运动,此时产生的感应电动势为:
同样给4分。](2)a棒固定、电键K闭合后,b棒自由下滑作切割磁感线运动,最终b棒以最大速度v2匀速运动,此时产生的感应电动势为:
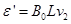 (6)
2分
(6)
2分
a棒与电阻R并联,再与b棒串联构成闭合电路,电流强度为
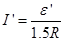 (7) 2分
(7) 2分
b棒受到的安培力与b棒重力平衡,有
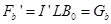 (8) 1分
(8) 1分
由(1)~(5)可解得: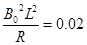 (9)
1分解(6)~(9),得
(9)
1分解(6)~(9),得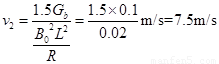 2分
2分
(3)电键K断开后,当磁场均匀变化时,在a、b棒与平行导轨构成的闭合回路内产生的感应电动势为
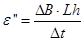 (10) 2分
(10) 2分
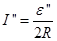 (11) 2分
(11) 2分
依题意,有
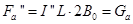 (12) 2分
(12) 2分
由(9)~(12)解得: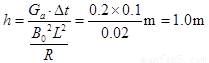 2分
2分
考点:电磁感应定律的综合应用
点评:难题。本题中导体切割磁感线运动或电路中磁通量的变化,产生感应电流,使导体受到安培力的作用,从而直接影响到导体的运动.本题中将产生感应电动势的那部分电路等效为电源,如果在一个电路中切割磁感线的是几部分互相联系的电路,则可等效成电源的串并联.分析内外电路结构,应用闭合电路欧姆定律和部分电路欧姆定律理顺电学量之间的关系。

 如图所示,在匀强磁场中有一个矩形单匝线圈ABCD,AB边与磁场垂直,MN边始终与金属滑环K相连,PQ边始终与金属滑环L相连.金属滑环L、交流电流表A、定值电阻R、金属滑环K通过导线串联.使矩形线圈以恒定角速度绕过BC、AD中点的轴旋转.下列说法中正确的是( )
如图所示,在匀强磁场中有一个矩形单匝线圈ABCD,AB边与磁场垂直,MN边始终与金属滑环K相连,PQ边始终与金属滑环L相连.金属滑环L、交流电流表A、定值电阻R、金属滑环K通过导线串联.使矩形线圈以恒定角速度绕过BC、AD中点的轴旋转.下列说法中正确的是( ) 如图所示,在匀强磁场中,水平放置两根平行金属导轨,导轨与大线圈甲相连,小线圈乙处于大线圈甲内,要使乙获得逆时针方向的持续电流,金属棒PQ在导轨上的运动情况应是向左
如图所示,在匀强磁场中,水平放置两根平行金属导轨,导轨与大线圈甲相连,小线圈乙处于大线圈甲内,要使乙获得逆时针方向的持续电流,金属棒PQ在导轨上的运动情况应是向左 如图所示,在匀强磁场中有竖直放置的两平行光滑导轨,其间距L=0.5m,导轨间接有一电阻.现有一质量为m=5×10-2kg的金属棒在重力和安培力作用下,水平地沿导轨匀速下滑,此时通过电阻的电流I=2A,它们接触良好,求:
如图所示,在匀强磁场中有竖直放置的两平行光滑导轨,其间距L=0.5m,导轨间接有一电阻.现有一质量为m=5×10-2kg的金属棒在重力和安培力作用下,水平地沿导轨匀速下滑,此时通过电阻的电流I=2A,它们接触良好,求: 如图所示,在匀强磁场中放置一个电阻不计的平行金属导轨,导轨跟大线圈M相连,导轨上放一根导线ab,磁感线垂直于导轨所在平面,欲使M所包围的小闭合线圈N产生顺时针方方的感应电流,则导线的运动情况可能是( )
如图所示,在匀强磁场中放置一个电阻不计的平行金属导轨,导轨跟大线圈M相连,导轨上放一根导线ab,磁感线垂直于导轨所在平面,欲使M所包围的小闭合线圈N产生顺时针方方的感应电流,则导线的运动情况可能是( ) 如图所示,在匀强磁场中,导体ab与光滑导轨紧密接触,ab在向右的拉力F作用下以速度v做匀速直线运动,当电阻R的阻值增大时,若速度v不变,则( )
如图所示,在匀强磁场中,导体ab与光滑导轨紧密接触,ab在向右的拉力F作用下以速度v做匀速直线运动,当电阻R的阻值增大时,若速度v不变,则( )