题目内容
【题目】质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角θ= 106o,轨道最低点为O,A点距水平面的高度h=0.8m。小物块离开C点后恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的滑动摩擦因数为μ1=0.33(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
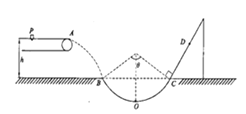
(1)小物块离开A点的水平初速度v1
(2)小物块经过O点时对轨道的压力
(3)斜面上CD间的距离
【答案】(1)![]()
(2)![]()
(3)![]()
【解析】
(1)对小物块,由A到B有:![]()
在B点![]() 所以
所以![]()
(2)对小物块,由B到O有
![]() 其中
其中![]()
在O点![]() 所以:N=43N
所以:N=43N
由牛顿第三定律知对轨道的压力为![]()
(3)物块沿斜面上滑:![]()
所以![]()
物块沿斜面下滑:![]()
由机械能守恒知![]()
小物块由C上升到最高点历时![]()
小物块由最高点回到D点历时![]()
故![]()
即![]()

练习册系列答案
相关题目