题目内容
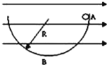
【题目】如图,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为1.5mg.求:
(1)小球受到的电场力的大小和方向.
(2)带电小球在滑动过程中的最大速度.
【答案】(1)![]() ,方向水平向右 (2)
,方向水平向右 (2)![]()
【解析】
(1) 设小球运动到最底位置B时速度为v,小球从A处沿槽滑到最底位置B的过程中,根据动能定理结合向心力公式联立方程即可求解;
(2) 小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,根据几何关系及动能定理即可求解
(1) 设小球运动到最底位置B时速度为v,此时
![]()
解得:![]()
若不受电场力,则
![]()
解得:![]()
因为v′>v
所以此过程中电场力做负功,电场力方向水平向右;
设电场力大小为F,由题意,小球从A处沿槽滑到最底位置B的过程中,根据动能定理得:
![]()
解得:![]() ,方向水平向右;
,方向水平向右;
(2) 小球在滑动过程中最大速度的条件:是小球沿轨道运动过程某位置时切向合力为零,设此时小球和圆心间的连线与竖直方向的夹角为θ,如图

mgsinθ=Fcosθ
解得:![]()
小球由A处到最大速度位置得过程中有:
![]()
解得:![]() 。
。

练习册系列答案
相关题目