��Ŀ����
����Ŀ����ͼ��ʾ�������Ϊ�� = 37����б��ĵ���һ���̶�����D����֪�����б��PO��Ķ�Ħ����������0.50��б�� OD���ֹ⻬��������Ȼ���ȵ����ʵ���һ�˹̶��� D�㣬��һ���� O�㣬PO�ij���L= 9.0m���� P����һ����Ϊ1kg��С���� A������Ϊ�ʵ㣩����ʹ A�Ӿ�ֹ��ʼ�»���g= 10m/s2��sin37��=0.6��cos37��=0.8����
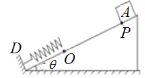
�������һ�νӴ�����ʱ������ٶȵĴ�С��
������֪���ɵ����ѹ����Ϊd=0.5m���ɵ����������Ep;
�������뵯�ɵ�һ�νӴ����������O����б��������������x;
�������뵯�ɽӴ����ٴκ������O����б��������������С��![]() .
.
���𰸡�(1)![]() (2)
(2)![]() (3)
(3) ![]() (4)4��
(4)4��
��������
(1)��PO�˶�����Ӧ�ö��ܶ���������⣻
(2)��O���������ѹ�������˶�����Ӧ�ö��ܶ���������⣻
(3)������O�ϻ��Ĺ���Ӧ�ö��ܶ�����⣻
(4)���ݶ��ܶ��������������߶Ⱥ���O���ٶȵĹ�ϵ�����������ε���O���ٶȵĹ�ϵ��Ȼ������˶�������⡣
(1)������PO�������ܵ���ֱ���µ���������ֱб�����ϵĵ���������б�����ϵ�Ħ�������˹���Ӧ�ö��ܶ����ã�![]()
���ԣ������һ�νӴ�����ʱ������ٶȵĴ�СΪ��![]()
(2)������O��������ѹ������̵Ĺ����У�ֻ�����������ɵ������������ɶ��ܶ����ɵõ��ɵ����������Ϊ��![]()
(3)����һ�δ�O�㵽������ѹ������ٵ���������ߵ�����У�
Ӧ�ö��ܶ����ã�![]()
��ã�![]()
(4)��������O���ٶ�Ϊv��ʱ����(3)��֪�����ݶ��ܶ���������������������Ϊ��![]() ��
��
�ɶ��ܶ����ɵ������ٴε���O����ٶ�v���У�![]()
��ã�![]()
������ÿ����һ��O�㣬������������Ϊ��һ�ε�![]() ��
��
���ԣ������һ�η���ʱ��б��������������Ϊ��![]()
���n����������������![]()
��Ϊ![]() ������n��4���������뵯�ɽӴ�4�κ������O����б��������������С��
������n��4���������뵯�ɽӴ�4�κ������O����б��������������С��![]() .
.

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�