题目内容
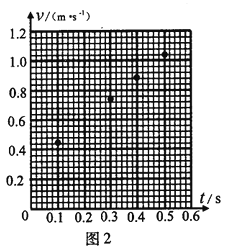
【题目】如图甲所示，间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上。在MNPQ矩形区域内有方向垂直于斜面的匀强磁场，磁感应强度为B；在CDEF矩形区域内有方向垂直于斜面向下的磁场，磁感应强度Bt随时间t变化的规律如图乙所示，其中Bt的最大值为2B。现将一根质量为M、电阻为R、长为L的金属细棒cd跨放在MNPQ区域间的两导轨上并把它按住，使其静止。在t=0时刻 ，让另一根长也为L的金属细棒ab从CD上方的导轨上由静止开始下滑，同时释放cd棒。已知CF长度为2L，两根细棒均与导轨良好接触，在ab从图中位置运动到EF处的过程中，cd棒始终静止不动，重力加速度为g；t0是未知量。求:
（1）通过cd棒的电流大小，并确定MNPQ区域内磁场的方向；
（2）当ab棒进入CDEF区域后，求cd棒消耗的电功率；
（3）ab棒刚下滑时离CD的距离。
【答案】（1）垂直于斜面向上（2）
（3）L
【解析】试题分析：（1）如图所示，由物体的平衡条件
cd棒： 
得
由于cd棒始终静止不动，说明回路中电流始终保持不变，而只有回路中电动势保持不变，才能保证电流不变，因此可以知道：在
时刻ab刚好到达CDEF区域的边界CD。
在0~
内，由楞次定律可知，回路中电流沿abdca方向，再由左手定则可知，
MNPQ区域内的磁场方向垂直于斜面向上
（2）ab、cd和导轨构成的回路中，ab相当于电源，
cd相当于外电阻， 
（3）ab进入CDEF区域前只受重力和支持力作用做匀加速运动，进入CDEF区域后将做匀速运动
设ab刚好到达CDEF区域的边界CD处的速度大小为v，刚下滑时离CD的距离为s 在0~
内：由法拉第电磁感应定律有E1=ΔΦ/Δt=（2B-B）（2L×L）/ t0=2BL2/ t0
在
后： 
，得
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
