Question

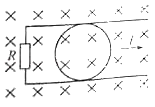
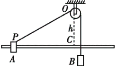
【题目】如图所示，足够长水平面的A点左侧光滑、右侧粗糙。宽度为r的物块P带有半径为r的四分之一光滑圆弧，圆弧的最低点切线水平，距地面的高度为1.5r，静止放在A点左侧适当位置。现让小球Q从物块P的圆弧最高点由静止释放，当小球Q落地的瞬间，物块P刚好与静止放在A点的小物块R发生弹性正碰，碰后小物块R运动的最远点C与A点的距离为3r 。已知P、Q、R的质量分别为6m、3m、2m，重力加速度为g，物块P、R碰撞过程时间很短，发生的位移不计，小球Q、物块R大小不计，求：

(1)小球Q离开P时的速度大小；

(2)小物块R与A点右侧水平面间的动摩擦因数；

(3)小球Q落地点B与A点的距离。

Answer 1

【答案】（1）（2）（3）4r

【解析】

（1）设Q 离开P时速度为vQ，此时P的速度为vP，Q从静止释放到离开P的过程中：

P、Q所组成的系统机械能守恒：

P、Q在水平方向上动量守恒：

联立相关各式解得：

（2）设R碰撞后R的速度为vR，P的速度为

P与R碰撞过程中动量守恒：

P与R发生弹性正碰，由能量守恒得：

对于R：在A到C的过程中，由动能定理得：

联立相关各式解得：

（3）设Q从离开P到落地所用时间为t，水平方向上运动位移为s1，P在时间t内运动位移为s2，Q落地点与A的距离为s3，

Q在此过程做平抛运动：

P在此过程做匀速直线运动：

因Q在离开P时与P右端相距r，故：s3= s1+ r+ s2

联立相关各式解得：s3=4r