题目内容
（17分）2007年3月1日，国家重大科学工程项目“EAST超导托卡马克核聚变实验装置”在合肥顺利通过了国家发改委组织的国家竣工验收。作为核聚变研究的实验设备，EAST可为未来的聚变反应堆进行较深入的工程和物理方面的探索，其目的是建成一个核聚变反应堆，届时从1升海水中提取氢的同位素氘，在这里和氚发生完全的核聚变反应，释放可利用能量相当于燃烧300公升汽油所获得的能量，这就相当于人类为自己制造了一个小太阳，可以得到无穷尽的清洁能源。作为核聚变研究的实验设备，要持续发生热核反应，必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内，约束的办法有多种，其中技术上相对较成熟的是用磁场约束核材料。如图所示为EAST部分装置的简化模型：垂直纸面的有环形边界的匀强磁场b区域，围着磁感应强度为零的圆形a区域，a区域内的离子向各个方向运动，离子的速度只要不超过某值，就不能穿过环形磁场的外边界而逃逸，从而被约束。设离子质量为m，电荷量为q，环形磁场的内半径为R1， 外半径R2 =（1+
）R1。
（1）将下列核反应方程补充完整，指出哪个属于核聚变方程。并求出聚变过程中释放的核能E0。已知
H的质量为m2，
H的质量为m3，α粒子的质量为mα，
的质量为mn，质子质量为mP，电子质量为me，光速为c。
A．
（ ） B．
( )
C．
( ) D．
( )
（2）若要使从a区域沿任何方向，速率为v的离子射入磁场时都不能越出磁场的外边界，则b区域磁场的磁感应强度B至少为多大?
（3）若b区域内磁场的磁感应强度为B，离子从a区域中心O点沿半径OM方向以某一速度射入b区，恰好不越出磁场的外边界。请画出在该情况下离子在a、b区域内运动一个周期的轨迹，并求出周期T。
解析：
（1）A属于聚变方程 （1分）
，2，
，
（全对得1分）
E = [m2＋m3－(mα＋mn)]c2 （1分）
（2）如图1所示，当离子的速度沿与内边界圆相切的方向射入磁场，且轨道与磁场外圆相切时所需磁场的磁感应强度B1，即为要求的值。设轨迹圆的半径为r1，
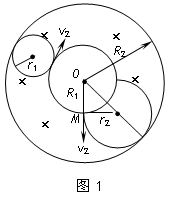
则r1＝
（1分）
由：qvB1＝m
（1分）
解之得：B1=
（2分）
（3）如图2所示（2分）。
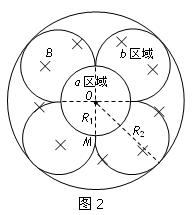
要使沿OM方向运动的离子不能穿越磁场，则其在环形磁场内的运动轨迹圆中最大值与磁场外边界圆相切。设这时轨迹圆的半径为r2，速度为v2，则：
r22 +R12＝（R2一r2）2 （1分）
解之得：r 2 ＝R1 （1分）
由qv2B＝m
解之得：v2 =
（1分）
离子在b区域中做匀速圆周运动的周期T1=
（1分）
离子在b区域中一次运动的时间t1 =
（1分）
离子在a区域中由O到M点的运动时间t2 =
（1分）
离子在a、b区域内运动的周期T= 4t1+8t2 =
（2分）
新课标快乐提优暑假作业陕西旅游出版社系列答案
)R1
的质量为m2，
H质量为m3，α粒子的质量为mα，
n的质量为mn，质子质量为mP，电子质量为me，光速为C．)
( )
( )
( )
( )
，外半径
．
．已知 
的质量为
， 
的质量为
。
粒子的质量为
的质量为
质子质量为
，电子质量为
，光速为c
B.
D.