Question

如图3-6-8所示，一细线的一端固定于倾角为θ=45° 的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球，试求当滑块以a=2g的加速度向左运动时细线的拉力T.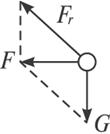

 图3-6-8

Answer 1

解析：本题是一个已知运动情况求未知力的问题.当滑块向左运动的加速度较小时，滑块对小球存在支持力，当滑块向左运动的加速度较大时，小球将脱离滑块斜面而“飘”起来.因此，本题还存在一个临界条件：当滑块向左移动的加速度为某一临界值时，斜面对小球的支持力恰好为零（小球将要离开斜面而“飘”起来），我们首先求此临界条件.此时小球受两个力：重力mg，绳的拉力T，根据牛顿第二定律的正交分解表示，有:

    Tcosθ=ma,                                                               ①

    Tsinθ-mg=0,                                                             ②

    联立①②两式并将θ=45°代入得a=g,

    即当斜面体滑块向左运动的加速度为a=g时，小球已“飘”起来了.

    此时小球受力情况如右图所示，故依据①②两式并将a=2g代入解得：T=mg，注意当小球“飘”起来时θ＜45°.

答案：mg