题目内容
如图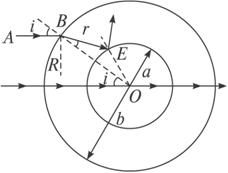
图
解析:根据对称性可知所求光束的截面应是一个圆,关键在于求出此圆的半径R.
设入射光线AB为所求光束的临界光线,入射角为i,经球壳外表面折射后折射角为r.因为AB为临界入射线,所以射向内表面的光线的入射角应正好等于临界角C.在△ABC中,由正弦定理得![]()
由于sinC=![]() ,n=
,n=![]() ,所以b=
,所以b=![]() asini.由几何关系可得
asini.由几何关系可得
R=bsini=a
所求平行光束的横截面积S=πR2=πa2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图
图
解析:根据对称性可知所求光束的截面应是一个圆,关键在于求出此圆的半径R.
设入射光线AB为所求光束的临界光线,入射角为i,经球壳外表面折射后折射角为r.因为AB为临界入射线,所以射向内表面的光线的入射角应正好等于临界角C.在△ABC中,由正弦定理得![]()
由于sinC=![]() ,n=
,n=![]() ,所以b=
,所以b=![]() asini.由几何关系可得
asini.由几何关系可得
R=bsini=a
所求平行光束的横截面积S=πR2=πa2.

 阅读快车系列答案
阅读快车系列答案