题目内容
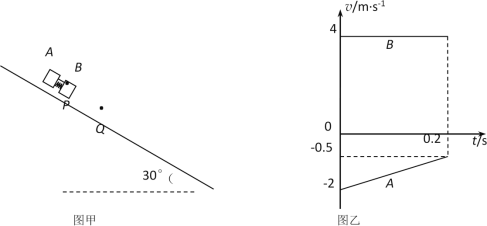
【题目】如图甲所示,足够长的斜面与水平面的夹角为![]() ,质量分别为0.5kg和1kg的A、B两个小物块,用一根细线相连,A、B之间有一被压缩的微型弹簧,A、B与弹簧组成的系统可视为质点。某时刻,将A、B从P点由静止释放,运动至Q点时,细线突然断裂,压缩的微型弹簧使A、B瞬间分离,从分离时开始计时,A、B短时间内运动的速度图像如图乙所示,重力加速度取g=10m/s。求:
,质量分别为0.5kg和1kg的A、B两个小物块,用一根细线相连,A、B之间有一被压缩的微型弹簧,A、B与弹簧组成的系统可视为质点。某时刻,将A、B从P点由静止释放,运动至Q点时,细线突然断裂,压缩的微型弹簧使A、B瞬间分离,从分离时开始计时,A、B短时间内运动的速度图像如图乙所示,重力加速度取g=10m/s。求:
(1)A、B与斜面间的动摩擦因数;
(2)细绳未断裂前微型弹簧储存的弹性势能;
(3)A、B再次相遇前的最远距离。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据图像可知,AB分离后,B沿斜面向下做匀速直线运动,A沿斜面向上做匀减速直线运动,且
![]()
对A由牛顿第二定律得
![]()
解得
![]()
对B由平衡方程得
![]()
解得
![]()
(2)细线断裂瞬间,对AB由动量守恒定律得
![]()
由能量守恒定律得
![]()
解得
![]()
(3)当AB的速度相等时,二者相距最远,设A上滑的时间为tA,位移为xA;A下滑过程中的加速度为![]() ,时间为
,时间为![]() ,位移为
,位移为![]() ,则有
,则有
![]() ,
,![]()
对A由牛顿第二定律得
![]()
![]() ,
,![]()
B发生的位移
![]()
AB再次相遇前的最远距离
![]()
解得
![]()

练习册系列答案
相关题目