[题目]在EF为边界的空间有一匀强磁场.磁感应强度大小为B.方向垂直于纸面向外.如图所示.纸面内有E.F.G三点.∠GEF=30°.∠EFG=135°先使带有电荷量为q(q>0)的点电荷a在纸面内垂直于EF从F点射入.其轨迹经过G点,再使另一个带有同样电荷量的点电荷b在纸面内与EF成一定角度从E点射入.其轨迹也经过G点.两点电荷从射出到经过G点所用的时间相题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在EF为边界的空间有一匀强磁场，磁感应强度大小为B，方向垂直于纸面向外。如图所示，纸面内有E、F、G三点，∠GEF=30°，∠EFG=135°先使带有电荷量为q（q>0）的点电荷a在纸面内垂直于EF从F点射入，其轨迹经过G点；再使另一个带有同样电荷量的点电荷b在纸面内与EF成一定角度从E点射入，其轨迹也经过G点，两点电荷从射出到经过G点所用的时间相同，且经过G点时的速度方向也相同。已知点电荷a的质量为m，轨道半径为R，不计重力，求：

(1)点电荷a从射出到经过G点所用的时间；

(2)求电荷b的质量mb；

(3)点电荷b的速度大小。

【答案】 (2)

【解析】（1）设点电荷a的速度大小为v，由牛顿第二定律的 ①

由①式得： ②

设点电荷a做圆周运动的周期为T，有 ③

如图，O和O1分别是a和b的圆轨道的圆心。

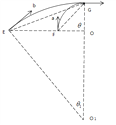
设a在磁场中偏转的角度为，由几何关系得 ④

故a从开始运动到经过G点所用的时间t为 ⑤

电荷b的速度大小为v1，轨道半径为R1，b在磁场中偏转的角度为，依题意有

⑥

由⑥式得

⑦

由于两轨道在G点相切，所以过G点的半径OG在同一直线上。由几何关系和题给条件得

⑧

R1=2R ⑨

联立②④⑦⑧⑩式，解得v1= ⑩

练习册系列答案

A. 感应电流所做的功为mgd

B. 感应电流所做的功为mg（d－L）

C. 当线圈的ab边刚进入磁场时速度最小

D. 线圈的最小速度可能为mgR/B2L2

【题目】已知通电长直导线周围某点的磁感应强度，即磁感应强度B与导线中的电流I成正比、与该点到导线的距离r成反比．如图所示，两根平行长直导线相距为R，通以大小、方向均相同的电流．规定磁场方向垂直纸面向里为正，在0﹣R区间内磁感应强度B随x变化的图线可能是（）

A. B. C. D.

【题目】设两极板正对面积为S，极板间的距离为d,静电计指针偏角为θ。实验中，极板所带电荷量不变，则下列说法正确的是 (　　)

A. 保持S不变，增大d,则θ变大

B. 用手触摸极板B,则θ变小

C. 保持d不变，减小S,则θ变小

D. 在两板间插入电介质,则θ变小

【题目】下列说法正确的是（）

A．牛顿进行了月—地实验，说明天上和地下的物体都遵从万有引力定律

B．根椐开普勒行星运动第三定律和匀速圆周运动公式，可以推导出，太阳对行星的引力(m为行星质量、r为行星运动半径)

C．卡文迪许利用扭秤装置测出静电力常量

D．伽利略研究自由落体运动时，通过上百次实验得到，只要斜面的倾角一定，小球从不同的高度开始滚动，小球的加速度是相同的。

【题目】如图所示，一根条形磁铁自左向右穿过一个闭合螺线管，则电路中( )

A. 始终有自a向b的感应电流流过电流表G

B. 先有a→G→b方向的感应电流，后有b→G→a方向的感应电流

C. 先有b→G→a方向的感应电流，后有a→G→b方向的感应电流

D. 将不会产生感应电流

【题目】如图所示，从高处由静止自由下落的小球自A处开始接触弹簧，到达B处时将弹簧压缩到最短，则在小球由A运动到B的过程中( )

A. 小球一直处于失重状态，动能逐渐增大

B. 合力对小球做负功，小球的速度一直减小

C. 小球的动能和重力势能之和保持不变

D. 小球的重力势能逐渐减小，弹簧的弹性势能逐渐增加

【题目】如图所示，在xOy平面内存在Ⅰ、Ⅱ、Ⅲ、Ⅳ四个场区，y轴右侧存在匀强磁场Ⅰ，y轴左侧与虚线MN之间存在方向相反的两个匀强电场，Ⅱ区电场方向竖直向下，Ⅲ区电场方向竖直向上，P点是MN与x轴的交点，OP为Ⅱ、Ⅲ场区的分界。有一质量为m、电荷量为q的带正电粒子由原点O以速度v0沿x轴正方向水平射入磁场Ⅰ，已知匀强磁场Ⅰ的磁感应强度垂直纸面向里、大小为B0，匀强电场Ⅱ和匀强电场Ⅲ的电场强度大小均为，如图所示，Ⅳ区的磁场垂直纸面向外、大小为，O、P之间的距离为，已知粒子最后能回到O点。粒子重力不计.

（1）求带电粒子从O点飞出后，第一次回到x轴时的位置坐标。

（2）根据题给条件画出粒子运动的轨迹。

（3）求带电粒子从O点飞出后到再次回到O点的时间。

【题目】如图所示，一根长 L = 3m 的光滑绝缘细直杆MN ，竖直固定在场强为 E =1.6 ×105N / C 、与水平方向成θ＝300角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球 A，电荷量Q＝+5×10－6C；另一带电小球 B 穿在杆上可自由滑动，电荷量q＝+2.0 ×10一6 C，质量m＝2.0×10一2 kg 。现将小球B从杆的上端N由静止释放。（静电力常量k＝9.0×109N·m2／C2，取 g =10m / s2）

（l）小球B开始运动时的加速度为多大？

（2）小球B从N端运动到速度最大时，匀强电场对小球B做了多少功？

（3）小球B从 N 端运动到距 M 端的高度 h2＝1.0m 时，速度为v＝1.5m / s ，求此过程中小球A对小球B的库仑力所做的功？

试题分类