题目内容
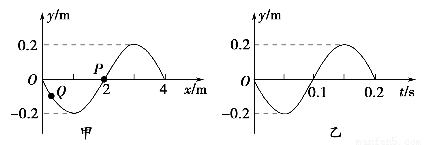
I.如图1甲为一列沿x轴传播的简谐横波在t=0时刻的波形图,A、B是波中的两个质点,图乙为质点B从该时刻起的振动图象.则下列判断正确的是
A.该波沿x轴正方向传播
B.该波的波速为10m/s
C.从该时刻起至A点第一次到达波谷所经历的时间为0.2s
D.经过半个周期质点B通过的路程比质点A通过的路程大
II.一个水池内盛有某种透明液体,液体的深度为H.在水池的底部中央放一点光源,其中一条光线以30°入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为105°,如图2所示.求:
(1)光在该液体中的传播速度大小;
(2)液体表面被光源照亮区域的面积.
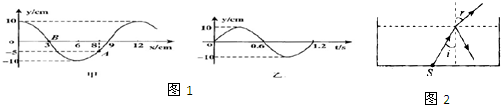
A.该波沿x轴正方向传播
B.该波的波速为10m/s
C.从该时刻起至A点第一次到达波谷所经历的时间为0.2s
D.经过半个周期质点B通过的路程比质点A通过的路程大
II.一个水池内盛有某种透明液体,液体的深度为H.在水池的底部中央放一点光源,其中一条光线以30°入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为105°,如图2所示.求:
(1)光在该液体中的传播速度大小;
(2)液体表面被光源照亮区域的面积.

分析:I、由振动图象和波动图象分别读出周期和波长.从振动图象读出t=0时刻质点B的振动方向,由判断出波传播方向.根据波形的平移法求A点第一次到达波谷所经历的时间.根据简谐运动的周期性可知,经过半个周期质点A、B路程相等.
II、(1)由题,已知入射角i=60°,折射角r=45°,根据折射定律求解该液体的折射率;
(2)当光恰好发生全反射,亮斑面积最大,由sinC=
可求出临界角,再由几何关系,可求出光斑面积.
II、(1)由题,已知入射角i=60°,折射角r=45°,根据折射定律求解该液体的折射率;
(2)当光恰好发生全反射,亮斑面积最大,由sinC=
| 1 |
| n |
解答:解:Ⅰ、A、由振动图象乙知,t=0时,B质点的振动方向向上,而在波动图象甲上,根据波形的平移判断可知,该波沿x轴正方向传播.故A正确.
B、由甲、乙图分别读出,λ=12cm=0.12m,T=1.2s,则v=
=0.1m/s.故B错误.
C、当图示时刻离A点最近的波谷传到A点时,A点第一次到达波谷,最近的波谷与A点平衡位置距离为x=8cm-6cm=2cm=0.02m
则经历的时间为t=
=
s=0.2s,故C正确.
D、A、B两质点都做简谐运动,振幅A相等,经过半个周期通过的路程都是2A=20cm.故D错误.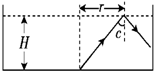
故选AC
Ⅱ、(1)由图知:入射角i=30°折射角r=45°
则折射率为n=
=
光在该液体中的传播速度大小v=
=
=2.12×108m/s
(2)若发生全反射,入射角C应满足
由sinC=
可得:C=45°
由题意知,液体被照亮区域为一个圆形区域,其半径为:R=HtanC=H
亮斑面积:S=πH2
答:(Ⅰ)AC;
(Ⅱ)光在该液体中的传播速度大小为2.12×108m/s;
(2)液体表面被光源照亮区域的面积是πH2.
B、由甲、乙图分别读出,λ=12cm=0.12m,T=1.2s,则v=
| λ |
| T |
C、当图示时刻离A点最近的波谷传到A点时,A点第一次到达波谷,最近的波谷与A点平衡位置距离为x=8cm-6cm=2cm=0.02m
则经历的时间为t=
| x |
| v |
| 0.02 |
| 0.1 |
D、A、B两质点都做简谐运动,振幅A相等,经过半个周期通过的路程都是2A=20cm.故D错误.

故选AC
Ⅱ、(1)由图知:入射角i=30°折射角r=45°
则折射率为n=
| sini |
| sinr |
| 2 |
光在该液体中的传播速度大小v=
| c |
| n |
| 3×108 | ||
|
(2)若发生全反射,入射角C应满足
由sinC=
| 1 |
| n |
由题意知,液体被照亮区域为一个圆形区域,其半径为:R=HtanC=H
亮斑面积:S=πH2
答:(Ⅰ)AC;
(Ⅱ)光在该液体中的传播速度大小为2.12×108m/s;
(2)液体表面被光源照亮区域的面积是πH2.
点评:第Ⅰ题关键要理解波动图象与振动图象的联系与区别,同时,读图要细心,数值和单位一起读.判断波的传播方向和质点的振动方向关系是必备的能力.
第Ⅱ题考查光的折射定律与光的全反射现象,运用几何知识来解题,同时注意全反射的条件.
第Ⅱ题考查光的折射定律与光的全反射现象,运用几何知识来解题,同时注意全反射的条件.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目