题目内容
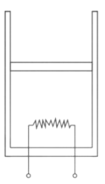
【题目】如图所示,一圆柱形绝热汽缸竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m,横截面积为S,与汽缸底部相距高度为h,此时封闭气体的温度为T。现通过很细电热丝缓慢加热气体,电热丝产生热量全部被气体吸收,电热丝两端电压为U,通过它的电流为I。经过时间t时,气体温度上升到1.5T。已知大气压强为p0,重力加速度为g,不计活塞与汽缸的摩擦,求:
①加热后活塞到汽缸底部的距离;
②加热过程中气体的内能增加量。
【答案】①h′=1.5h;②△U=UIt-0.5h(p0S+mg)
【解析】
①封闭发生等压变化,活塞横截面积为S,初态体积V1=hS,温度T1=T,
末态体积V2=h′S,温度T2=1.5T
根据盖一吕萨克定律可得
![]()
解得加热后活塞到汽缸底部的距离
h′=1.5h
②根据受力平衡可得封闭气体的压强
![]()
升温过程对外做功
W=-p(h′-h)S
热力学第一定律
△U=W+Q
又
Q=UIt
联立可得
△U=UIt-0.5h(p0S+mg)

练习册系列答案
相关题目