题目内容
11．
如图为一压路机的示意图，其大轮半径是小轮半径的1.5倍．A、B分别为大轮和小轮边缘上的点．在压路机前进时（ ）| A． | A、B两点的线速度之比vA：vB=1：1 | |
| B． | A、B两点的线速度之比vA：vB=3：2 | |
| C． | A、B两点的角速度之比ωA：ωB=3：2 | |
| D． | A、B两点的向心加速度之比aA：aB=2：3 |
分析 压路机前进时，其轮子边缘上的点线速度大小相等，根据公式v=rω求解角速度之比．由a=$\frac{{v}^{2}}{r}$求解向心加速度之比．
解答 解：AB、压路机前进时，其轮子边缘上的点参与两个分运动，即绕轴心的转动和随着车的运动；与地面接触点速度为零，故两个分运动的速度大小相等、方向相反，故A、B两点圆周运动的线速度都等于汽车前进的速度，故A、B两点的线速度之比vA：vB=1：1，故A正确，B错误；
C、A、B两点的线速度之比vA：vB=1：1，根据公式v=rω，线速度相等时，角速度与半径成反比，故A、B两点的角速度之比ωA：ωB=2：3，故C错误；
D、A、B两点的线速度之比vA：vB=1：1，由a=$\frac{{v}^{2}}{r}$知，向心加速度之比aA：aB=2：3，故D正确．
故选：AD．
点评 本题关键是明确轮子转动线速度相等，然后根据公式v=rω和a=$\frac{{v}^{2}}{r}$分析．
练习册系列答案
相关题目
现要测定一个额定电压6V、额定功率3W的小灯泡的伏安特性曲线．要求所测电压范围为0V～5.5V．
2．
如图所示的含有变压器的交流电路中，A1、A2都是理想交流电流表，已知变压器原副线圈匝数比为n1：n2=10：1，则（ ）
如图所示的含有变压器的交流电路中，A1、A2都是理想交流电流表，已知变压器原副线圈匝数比为n1：n2=10：1，则（ ）| A． | I1：I2=1：1 | B． | I1：I2=1：10 | C． | I1：I2=10：1 | D． | 无法确定 |
16．在双缝干涉实验中发现条纹太密，难以测量，可以采用的改善办法是（ ）
| A． | 改用波长较短的光作为入射光 | B． | 增大双缝间距 | ||
| C． | 减少双缝间距 | D． | 增大双缝到屏的距离 |
3．
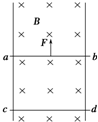一空间有垂直纸面向里的匀强磁场B，两条电阻不计的平行光滑导轨竖直放置在磁场内，如图所示，磁感应强度B=0.5T，导体棒ab、cd长度均为0.2m，电阻均为0.1Ω，重力均为0.1N，现用力向上拉动导体棒ab，使之匀速上升（导体棒ab、cd与导轨接触良好），此时cd静止不动，则ab上升时，下列说法不正确的是（ ）
一空间有垂直纸面向里的匀强磁场B，两条电阻不计的平行光滑导轨竖直放置在磁场内，如图所示，磁感应强度B=0.5T，导体棒ab、cd长度均为0.2m，电阻均为0.1Ω，重力均为0.1N，现用力向上拉动导体棒ab，使之匀速上升（导体棒ab、cd与导轨接触良好），此时cd静止不动，则ab上升时，下列说法不正确的是（ ）| A． | ab受到的拉力大小为0.2N | |
| B． | ab向上运动的速度为2m/s | |
| C． | 在2s内，拉力做的功有0.4J的能转化为电能 | |
| D． | 在2s内，拉力做功为0.6J |
