题目内容
两个等量同种电荷固定于光滑水平面上,其连线的中垂线上有A、B、C三点,如图甲所示.一个电荷量为2×l0 -6C、质量为lg的小物块从该水平面内的C点静止释放,其运动的v-t图象如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的是 ( )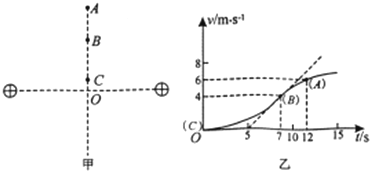

| A、B为中垂线上电场强度最大的点,其电场强度E=l×l03V/m | B、由C到A的过程中,物块的电势能先减小后变大 | C、由C到A的过程中,电势逐渐升高 | D、AB两点电势差UAB=-5×103V |
分析:根据v-t图象的斜率等于加速度和牛顿第二定律求解电场强度E.根据能量守恒定律分析物块电势能的变化情况.根据电场线方向判断电势的高低.根据动能定理求解AB两点电势差UAB.
解答:解:
A、v-t图象的斜率等于加速度,B点处为整条图线切线斜率最大的位置,说明B为中垂线上加速度最大的点,根据牛顿第二定律得:F=qE=ma知,B为中垂线上电场强度最大的点,B点的加速度为 a=
=
=2m/s2,E=
=
V/m=l×l03V/m.故A正确.
B、由图知,由C到A的过程中,物块的速度不断增大,动能增大,根据能量守恒得:物块的电势能不断减小.故B错误.
C、由电势能的公式EP=qφ知,由C到A的过程中,电势逐渐降低,故C错误.
D、物块从A到B的过程,根据动能定理得:qUAB=
m
-
m
则得,UAB=
m(
-
)=
×(42-62)V=-5×103V,故D正确.
故选:AD
A、v-t图象的斜率等于加速度,B点处为整条图线切线斜率最大的位置,说明B为中垂线上加速度最大的点,根据牛顿第二定律得:F=qE=ma知,B为中垂线上电场强度最大的点,B点的加速度为 a=
| △v |
| △t |
| 4 |
| 2 |
| ma |
| q |
| 10-3×2 |
| 2×10-6 |
B、由图知,由C到A的过程中,物块的速度不断增大,动能增大,根据能量守恒得:物块的电势能不断减小.故B错误.
C、由电势能的公式EP=qφ知,由C到A的过程中,电势逐渐降低,故C错误.
D、物块从A到B的过程,根据动能定理得:qUAB=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
则得,UAB=
| 1 |
| 2q |
| v | 2 B |
| v | 2 A |
| 10-3 |
| 2×2×10-6 |
故选:AD
点评:解决本题关键是掌握速度图象的物理意义和动能定理,知道电势与电势能的关系EP=qφ.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
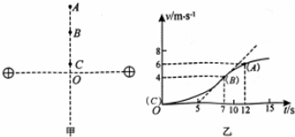 两个等量同种电荷固定于光滑水平面上,其连线的中垂线上有A、B、C三点,如图甲所示.一个电荷量为2×l0-6C、质量为lg的小物块从该水平面内的C点静止释放,其运动的v-t图象如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的是 ( )
两个等量同种电荷固定于光滑水平面上,其连线的中垂线上有A、B、C三点,如图甲所示.一个电荷量为2×l0-6C、质量为lg的小物块从该水平面内的C点静止释放,其运动的v-t图象如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的是 ( )| A、B为中垂线上电场强度最小的点,其电场强度E=l×l03V/m | B、由C到A的过程中,物块的电势能先减小后变大 | C、由C到A的过程中,电势逐渐升高 | D、AB两点间的电势差大小为5×103V |
如图甲所示,两个等量同种电荷固定于光滑水平面上,其连线中垂线上有A、B、C三点,一个电荷量q=2C,质量m=1kg的小物块从C点由静止释放,其仅在电场力作用下运动的v-t图象如图乙所示,其中B点处为整条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的是( )
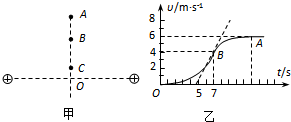

| A、A、B两点的电势差UAB=-5V | B、由C点到A点的过程中,电势逐渐升高 | C、由C点到A点的过程中,物块电势能先减小后变大 | D、B点为中垂线上电场强度最大的点,场强E=2 V/m |
 两个等量同种电荷固定于光滑水平面上,其连线中垂线上有A、B、C三点,如图甲所示.一个电 量为2C,质量为1kg的小物块从C点静止释放,其运动的v~t图象如图乙所示,其中B点处为整 条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的( )
两个等量同种电荷固定于光滑水平面上,其连线中垂线上有A、B、C三点,如图甲所示.一个电 量为2C,质量为1kg的小物块从C点静止释放,其运动的v~t图象如图乙所示,其中B点处为整 条图线切线斜率最大的位置(图中标出了该切线).则下列说法正确的( )