题目内容
【题目】如图所示,方形木箱质量为M,其内用两轻绳将一质量m=0.1kg的小球悬挂于P、Q两点,两细绳与水平的车顶面的夹角为60°和30°.水平传送带AB长l=30m,以v=15m/s的速度顺时针转动,木箱与传送带间动摩擦因数μ=0.75,(g=10m/s2)求: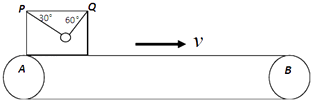
(1)设木箱为质点,且木箱由静止放到传送带上,那么经过多长时间木箱能够从A运动到传送带的另一端B处;
(2)木箱放到传送带A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为多少?
【答案】
(1)解:木箱由静止放到传送带上,开始过程,根据牛顿第二定律得
对木箱:μMg=Ma
a=7.5m/s2
木箱加速位移: ![]() x1=15m
x1=15m
木箱加速时间: ![]()
x1=15m<l=30m 所以还要在传送带上匀速后一段距离
木箱匀速时运动的时间:l﹣x1=vt2 t2=1s
所以木箱从A运动到传送带另一端B处经历时间t=t1+t2=3s
答:木箱由静止放到传送带上,经过3s时间木箱能够从A运动到传送带的另一端B处
(2)解:设绳P伸直恰好无拉力时木箱的加速度为a0,则由牛顿第二定律得
mgtan30°=ma0
代入解得 ![]()
木箱加速时a=7.5m/s2> ![]()
所以小球已经°故绳P的张力大小TP=0
此时: ![]() =ma
=ma
代入解得TQ=1.25N
答:木箱放到传送带A点后,在木箱加速的过程中,绳P和绳Q的张力大小分别为0和1.25N
【解析】(1)木箱由静止放到传送带上,水平方向先做受到滑动摩擦力,做匀加速直线运动,由牛顿第二定律求出加速度,由速度公式求出木箱速度与传送带相同时经历的时间和通过的位移,并判断木箱是否有匀速运动过程.如有,求出时间,再求总时间.(2)由牛顿第二定律求出绳P恰好张力时木箱的加速度a0,根据a0与木箱加速过程的加速度a的大小比较,判断绳P是否有张力,再由牛顿第二定律求解两绳的张力.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案