题目内容
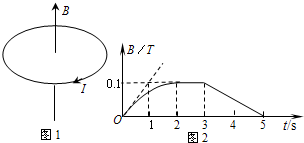 在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,线圈所围的面积为0.1m2,线圈电阻为1Ω.规定线圈中感应电流I 的正方向从上往下看是顺时针方向,如图1所示.磁场的磁感应强度B随时间t的变化规律如图2所示.则以下说法正确的是( )
在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,线圈所围的面积为0.1m2,线圈电阻为1Ω.规定线圈中感应电流I 的正方向从上往下看是顺时针方向,如图1所示.磁场的磁感应强度B随时间t的变化规律如图2所示.则以下说法正确的是( )分析:根据楞次定律判断感应电流的方向,通过法拉第电磁感应定律E=n
S求出感应电动势的大小,结合闭合电路欧姆定律求出电流的大小.
| △B |
| △t |
解答:解:A、根据闭合电路欧姆定律得,I=
=n
,知磁感应强度的变化率越大,则电流越大,磁感应强度变化率最大值为0.1,则最大电流I=
A=0.01A.故A错误.
B、根据楞次定律知,感应电流的方向先顺时针后逆时针方向.故B正确.
C、当电流最大时,发热功率最大,则P=I2R=0.012×1=1×10-4W.故C正确.
D、根据q=
△t=
,因为在0~5s内磁通量的变化量为零,则通过线圈某截面的总电量为零.故D正确.
故选BCD.
| E |
| R |
| △BS |
| △tR |
| 0.1×0.1 |
| 1 |
B、根据楞次定律知,感应电流的方向先顺时针后逆时针方向.故B正确.
C、当电流最大时,发热功率最大,则P=I2R=0.012×1=1×10-4W.故C正确.
D、根据q=
. |
| I |
| n△Φ |
| R |
故选BCD.
点评:解决本题的关键会运用法拉第电磁感应定律求解电动势的大小,会运用楞次定律判断感应电流的方向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
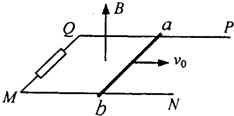 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )| A、电阻R上产生的焦耳热 | B、通过电阻R的总电荷量 | C、ab棒运动的位移 | D、ab棒运动的时间 |
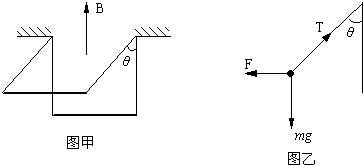
 如图所示,在竖直向上的匀强磁场中,有一倾角为θ的光滑轨道,在垂直轨迹方向上置有一长度L、质量为m的导体棒ab,当ab中通有图示方向的电流时,导体棒处于静止状态,求:
如图所示,在竖直向上的匀强磁场中,有一倾角为θ的光滑轨道,在垂直轨迹方向上置有一长度L、质量为m的导体棒ab,当ab中通有图示方向的电流时,导体棒处于静止状态,求: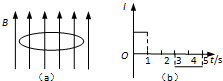 如图(a)所示,在竖直向上的匀强磁场中,水平放置一个不变形的铜圆环,规定从上向下看时,铜环中的感应电流I沿顺时针方向为正方向.图(b)表示铜环中的感应电流I随时间t变化的图象,则磁场B随时间t变化的图象可能是下图中的( )
如图(a)所示,在竖直向上的匀强磁场中,水平放置一个不变形的铜圆环,规定从上向下看时,铜环中的感应电流I沿顺时针方向为正方向.图(b)表示铜环中的感应电流I随时间t变化的图象,则磁场B随时间t变化的图象可能是下图中的( ) 如图所示,质量为m=50g的铜棒长L=10cm,用长度均为l,质量可不计的两根软导线水平地悬吊在竖直向上的匀强磁场B中,已知B=0.50T,通电后棒向纸外偏转,当棒处于静止状态时,悬线与竖直方向的夹角为θ=37°.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求铜棒中电流的方向及电流的大小.
如图所示,质量为m=50g的铜棒长L=10cm,用长度均为l,质量可不计的两根软导线水平地悬吊在竖直向上的匀强磁场B中,已知B=0.50T,通电后棒向纸外偏转,当棒处于静止状态时,悬线与竖直方向的夹角为θ=37°.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求铜棒中电流的方向及电流的大小.