题目内容
5.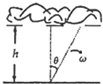 探照灯照射在云层底面上,底面是与地面平行的平面,如图所示,云层底面高h,探照灯以角速度ω在竖直平面内转动,当光束转过与竖直方向夹角为θ时,此刻云层底面上光点的移动速度是( )
探照灯照射在云层底面上,底面是与地面平行的平面,如图所示,云层底面高h,探照灯以角速度ω在竖直平面内转动,当光束转过与竖直方向夹角为θ时,此刻云层底面上光点的移动速度是( )| A. | $\frac{h}{cosθ}•ω$ | B. | $\frac{htanθ}{θ}•ω$ | C. | $\frac{h}{si{n}^{2}θ}•ω$ | D. | $\frac{h}{co{s}^{2}θ}$•ω |
分析 求出光束转到与竖直方向夹角为θ时,光点转动的线速度,该线速度等于光点移动速度垂直于半径方向上的分速度,根据平行四边形定则求出云层底面上光点的移动速度.
解答 解:当光束转过θ角时,光照射在云层上的位置到灯的距离为L=$\frac{h}{cosθ}$,
将光点的速度分解为垂直于L方向和沿L方向,这个位置光束的端点沿切线方向的线速度为v=ωL
则云层底面上光点的移动速度为v′=$\frac{v}{cosθ}$=$\frac{hω}{co{s}^{2}θ}$.
故选:D
点评 解决本题的关键知道光点转动的线速度为云层底面上光点的移动速度垂直半径半径方向上的线速度,根据平行四边形定则求出合速度的大小.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
4.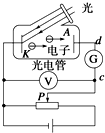 用图所示的光电管研究光电效应的实验中,用某种频率的单色光a照射光电管阴极K,电流计G的指针发生偏转.而用另一频率的单色光b照射光电管阴极K时,电流计G的指针不发生偏转,那么( )
用图所示的光电管研究光电效应的实验中,用某种频率的单色光a照射光电管阴极K,电流计G的指针发生偏转.而用另一频率的单色光b照射光电管阴极K时,电流计G的指针不发生偏转,那么( )
 用图所示的光电管研究光电效应的实验中,用某种频率的单色光a照射光电管阴极K,电流计G的指针发生偏转.而用另一频率的单色光b照射光电管阴极K时,电流计G的指针不发生偏转,那么( )
用图所示的光电管研究光电效应的实验中,用某种频率的单色光a照射光电管阴极K,电流计G的指针发生偏转.而用另一频率的单色光b照射光电管阴极K时,电流计G的指针不发生偏转,那么( )| A. | a光的频率一定小于b光的频率 | |
| B. | 增加b光的强度可能使电流计G的指针发生偏转 | |
| C. | 用a光照射光电管阴极K时通过电流计G的电流是由d到c | |
| D. | 只增加a光的强度可使通过电流计G的电流增大 |
20.如图所示为氢原子能级图,可见光的光子能量范围约为1.62eV~3.11eV.下列说法正确的是( )
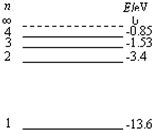

| A. | 大量处在n>2的高能级的氢原子向n=2能级跃迁时,发出的光可能是紫外线 | |
| B. | 大量处在n=3的氢原子向n=2能级跃迁时,发出的光具有荧光效应 | |
| C. | 大量处在n=3能级的氢原子向n=1能级跃迁时,发出的光是红外线 | |
| D. | 处在n=2能级的氢原子吸收任意频率的可见光的光子都能发生电离 |
17.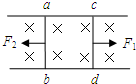 如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
 如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )| A. | F1>F2 | B. | F1=F2 | C. | Uab>Ucd | D. | Uab=Ucd |
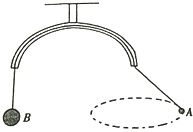 如图所示,内壁光滑的弯曲钢管固定在天花板上,一根结实的细绳穿过钢管,两端分别拴着一个小球A和B.小球A和B的质量之比$\frac{{m}_{A}}{{m}_{B}}$=$\frac{1}{2}$.当小球A在水平面内做匀速圆周运动时,小球A到管口的绳长为l,此时小球B恰好处于平衡状态.管子的内径粗细不计,重力加速度为g.试求:
如图所示,内壁光滑的弯曲钢管固定在天花板上,一根结实的细绳穿过钢管,两端分别拴着一个小球A和B.小球A和B的质量之比$\frac{{m}_{A}}{{m}_{B}}$=$\frac{1}{2}$.当小球A在水平面内做匀速圆周运动时,小球A到管口的绳长为l,此时小球B恰好处于平衡状态.管子的内径粗细不计,重力加速度为g.试求: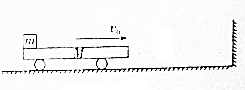 如图所示,质量为M=1kg的平板小车的左端放着一个质量为m=3kg的小铁块,铁块和小车之间的动摩擦因数为μ=0.5.开始时,小车和铁块一起以速度v=3m/s在光滑水平地面上向右运动,之后小车与墙壁发生碰撞,碰撞时间极短,碰撞后小车原速率反向弹回.车身足够长,使得铁块不会与墙相碰,也不会从车上落下(g取10m/s2).求:
如图所示,质量为M=1kg的平板小车的左端放着一个质量为m=3kg的小铁块,铁块和小车之间的动摩擦因数为μ=0.5.开始时,小车和铁块一起以速度v=3m/s在光滑水平地面上向右运动,之后小车与墙壁发生碰撞,碰撞时间极短,碰撞后小车原速率反向弹回.车身足够长,使得铁块不会与墙相碰,也不会从车上落下(g取10m/s2).求:


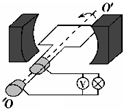 发电机转子是n匝边长为L的正方形线圈,将它置于磁感应强度为B的匀强磁场中,绕垂直于磁场方向的轴以角速度ω做匀速转动,转动开始时线圈平面与磁场方向平行,已知线圈的总电阻为r,外电路的电阻为R.试求:
发电机转子是n匝边长为L的正方形线圈,将它置于磁感应强度为B的匀强磁场中,绕垂直于磁场方向的轴以角速度ω做匀速转动,转动开始时线圈平面与磁场方向平行,已知线圈的总电阻为r,外电路的电阻为R.试求: