题目内容
20.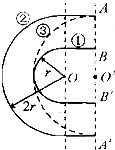 用物理模型的方法研究赛车过弯道的技术.假设赛车场的一段弯道如图所示,转弯处为圆心在O点的半圆,内外半径分别为r和2r,图中直线ABB'A'到圆心O的距离等于r.有一辆赛车(看成质点)要以图中线段AB为起点,经弯道到达线段A'B'.比较如图所示的三条路线:路线①沿赛道最内侧从B到B',路线②沿赛道最外侧从A到A',路线③是以BB'的中点O'为圆心的半圆.已知选择不同路线时,在垂直赛车速度方向上路面对轮胎的最大静摩擦大小都一样,且赛车沿每一路线行驶的全程都以过本路线中的圆弧时不打滑的最大速率匀速行驶.下列研究结果正确的是( )
用物理模型的方法研究赛车过弯道的技术.假设赛车场的一段弯道如图所示,转弯处为圆心在O点的半圆,内外半径分别为r和2r,图中直线ABB'A'到圆心O的距离等于r.有一辆赛车(看成质点)要以图中线段AB为起点,经弯道到达线段A'B'.比较如图所示的三条路线:路线①沿赛道最内侧从B到B',路线②沿赛道最外侧从A到A',路线③是以BB'的中点O'为圆心的半圆.已知选择不同路线时,在垂直赛车速度方向上路面对轮胎的最大静摩擦大小都一样,且赛车沿每一路线行驶的全程都以过本路线中的圆弧时不打滑的最大速率匀速行驶.下列研究结果正确的是( )| A. | 若选择路线①,则赛车运动的路程最短 | |
| B. | 若选择路线②,则赛车的运动速率最小 | |
| C. | 若选择路线③,则赛车运动的时间最短 | |
| D. | 在三条路线的圆弧上,赛车的向心加速度大小都相等 |
分析 根据几何关系得出路程的大小从而进行比较.根据最大静摩擦力,结合牛顿第二定律得出最大速率,从而比较运动的时间.根据向心加速度公式比较三段路线的向心加速度关系
解答 解:A、选择路线①,经历的路程 s1=2r+πr,选择路线②,经历的路程s2=2πr+2r,选择路线③,经历的路程s3=2πr,可知选择路线①,赛车经过的路程最短,故A正确.
B、根据Fmax=m$\frac{{v}^{2}}{r}$得,v=$\sqrt{\frac{{F}_{max}r}{m}}$,Fmax一样,则知选择路线①,轨道半径最小,则速率最小,故B错误.
C、根据v=$\sqrt{\frac{{F}_{max}r}{m}}$知,通过①、②、③三条路线的最大速率之比为1:$\sqrt{2}$:$\sqrt{2}$,根据t=$\frac{s}{v}$,由三段路程可知,选择路线③,赛车所用时间最短,故C正确.
D、根据a=$\frac{{v}^{2}}{r}$知,因为最大速率之比为1:$\sqrt{2}$:$\sqrt{2}$,半径之比为1:2:2,则三条路线上,赛车的向心加速度大小相等.故D正确.
故选:ACD
点评 本题考查了圆周运动向心加速度、向心力在实际生活中的运用,知道汽车做圆周运动,靠静摩擦力提供向心力,抓住最大静摩擦力相等求出最大速率之比是关键.

练习册系列答案
相关题目
8.如图所示闭合电路,当滑动变阻器滑动头P向右移动的过程中,下面判断正确的是( )


| A. | 电灯亮度变亮,电流表读数增大 | B. | 电灯亮度变暗,电流表读数不变 | ||
| C. | 电灯亮度不变,电流表读数不变 | D. | 电灯亮度变亮,电流表读数变小 |
8. 如图所示,“蹦极”运动中,游戏者身系弹性绳下落,不计空气阻力,游戏者从图中位置下落到最低点过程中,下列说法正确的是( )
如图所示,“蹦极”运动中,游戏者身系弹性绳下落,不计空气阻力,游戏者从图中位置下落到最低点过程中,下列说法正确的是( )
 如图所示,“蹦极”运动中,游戏者身系弹性绳下落,不计空气阻力,游戏者从图中位置下落到最低点过程中,下列说法正确的是( )
如图所示,“蹦极”运动中,游戏者身系弹性绳下落,不计空气阻力,游戏者从图中位置下落到最低点过程中,下列说法正确的是( )| A. | 弹性绳原长位置,弹性绳弹力等于游戏者重力 | |
| B. | 游戏者速度最大时,弹性绳的弹性势能为零 | |
| C. | 弹性绳的弹性势能最大时,游戏者速度为零 | |
| D. | 弹性绳的弹性势能先增大后减小,游戏者的动能一直增大 |
12.一物体做匀变速直线运动,当t=0时,物体的速度大小为10m/s,方向向东,当t=2s时,物体的速度大小为8m/s,方向仍向东,则当t为多少时,物体的速度大小变为2m/s( )
| A. | 9s | B. | 12s | C. | 7s | D. | 8s |
9.对于匀速圆周运动的物体,下列物理量中不断变化的是( )
| A. | 线速度 | B. | 角速度 | C. | 周期 | D. | 加速度 |
10.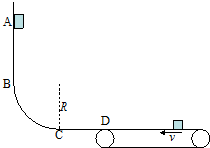 如图所示,光滑轨道ABCD中BC为四分之一圆弧,圆弧半径为R,CD部分水平,末端D点与右端足够长的水平传送带无缝连接,传送带以恒定速度v逆时针转动.现将一质量为m的小滑块从轨道上A点由静止释放,A到C的竖直高度为H,则( )
如图所示,光滑轨道ABCD中BC为四分之一圆弧,圆弧半径为R,CD部分水平,末端D点与右端足够长的水平传送带无缝连接,传送带以恒定速度v逆时针转动.现将一质量为m的小滑块从轨道上A点由静止释放,A到C的竖直高度为H,则( )
 如图所示,光滑轨道ABCD中BC为四分之一圆弧,圆弧半径为R,CD部分水平,末端D点与右端足够长的水平传送带无缝连接,传送带以恒定速度v逆时针转动.现将一质量为m的小滑块从轨道上A点由静止释放,A到C的竖直高度为H,则( )
如图所示,光滑轨道ABCD中BC为四分之一圆弧,圆弧半径为R,CD部分水平,末端D点与右端足够长的水平传送带无缝连接,传送带以恒定速度v逆时针转动.现将一质量为m的小滑块从轨道上A点由静止释放,A到C的竖直高度为H,则( )| A. | 滑块在传送带上向右运动的最大距离与传送带速度V的大小无关 | |
| B. | 小滑块不可能返回A点 | |
| C. | 若H=4R,滑块经过C点时对轨道压力大小为8mg | |
| D. | 若H=4R,皮带速度v=$\sqrt{2gR}$,则物块第一次滑上传送带由于摩擦而产生的内能为9mgR |
 为了固定竖直立柱,用绳按如图3-49方法缠绕立柱,绳的两端A.B固定在地面上,绳OA.OB.OC在同一平面内.绳OA,OB,OC在同一平面内.绳OA,OB长度相同,所受地面拉力大小均为F,两绳夹角为90度.求绳OC所受立柱的拉力大小.
为了固定竖直立柱,用绳按如图3-49方法缠绕立柱,绳的两端A.B固定在地面上,绳OA.OB.OC在同一平面内.绳OA,OB,OC在同一平面内.绳OA,OB长度相同,所受地面拉力大小均为F,两绳夹角为90度.求绳OC所受立柱的拉力大小.