��Ŀ����
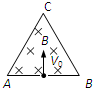
 ��ͼ��ʾ��һ���̶��ĵ��Եȱ������ο��ABC���߳�ΪL���ڿ����д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����AB�ߵ��е���һ��С�ף�������һ������Ϊ+q������Ϊm�Ҳ���������������ijһ���ٶȴ�ֱ��AB������ڣ�������ڱڴ�ֱ��ײ����������������䣬��ײʱ����Բ��ƣ��������ɴ���������ײ���ִ�������������
��ͼ��ʾ��һ���̶��ĵ��Եȱ������ο��ABC���߳�ΪL���ڿ����д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����AB�ߵ��е���һ��С�ף�������һ������Ϊ+q������Ϊm�Ҳ���������������ijһ���ٶȴ�ֱ��AB������ڣ�������ڱڴ�ֱ��ײ����������������䣬��ײʱ����Բ��ƣ��������ɴ���������ײ���ִ���������������1����������ڵ����������ʱ���Լ���Ӧ�ij��ٶ�V0��
��2���������������ij��ٶȼ���Ӧ�Ŀ����˶�ʱ��ı���ʽ��
��������1��������ų���������Բ���˶��������������ο����ײ����ʱ���˶�ʱ����̣������켣��������ڣ��ٵõ����ʱ�䣮�ɼ���֪ʶ����켣�İ뾶����ţ�ٵڶ�����������ٶȣ�
��2�������켣���ܵ���������ݼ���֪ʶ�õ��켣�뾶�������α߳��Ĺ�ϵ����ţ�ٵڶ����ɼ��������ٶ��������������ʱ�������ڵĹ�ϵ���ʱ�䣮
��2�������켣���ܵ���������ݼ���֪ʶ�õ��켣�뾶�������α߳��Ĺ�ϵ����ţ�ٵڶ����ɼ��������ٶ��������������ʱ�������ڵĹ�ϵ���ʱ�䣮
���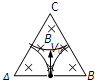 �⣺��1����ͼ����ʱ�����֪������AC��BC�߸���ײһ�κ��AB��С�ɳ���ֱ��У�
�⣺��1����ͼ����ʱ�����֪������AC��BC�߸���ײһ�κ��AB��С�ɳ���ֱ��У�
tmin=
T=
��Ӧ�İ뾶Ϊ��Rmax=
L=
��ã�v0=
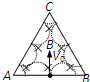 ��2����ͼ��R��L֮��������ʽ���ɣ�
��2����ͼ��R��L֮��������ʽ���ɣ�
R��2n+1��=
L������n=0��1��2����
���ã�R=
=
��ã�v0=
��n=0��1��2����
t=
T+3nT=
(6n+1)��n=0��1��2����
��
��1����������ڵ����������ʱ��Ϊ
����Ӧ�ij��ٶ�v0��
��
��2���������������ij��ٶ���
��n=0��1��2��������Ӧ�Ŀ����˶�ʱ��ı���ʽΪt=
T+3nT=
(6n+1)��n=0��1��2������
 �⣺��1����ͼ����ʱ�����֪������AC��BC�߸���ײһ�κ��AB��С�ɳ���ֱ��У�
�⣺��1����ͼ����ʱ�����֪������AC��BC�߸���ײһ�κ��AB��С�ɳ���ֱ��У�tmin=
| 1 |
| 2 |
| ��m |
| Bq |
��Ӧ�İ뾶Ϊ��Rmax=
| 1 |
| 2 |
| mv0 |
| Bq |
��ã�v0=
| BqL |
| 2m |
 ��2����ͼ��R��L֮��������ʽ���ɣ�
��2����ͼ��R��L֮��������ʽ���ɣ�R��2n+1��=
| 1 |
| 2 |
���ã�R=
| L |
| 2(2n+1) |
| mv0 |
| Bq |
��ã�v0=
| BqL |
| 2(2n+1)m |
t=
| 1 |
| 2 |
| ��m |
| Bq |
��
��1����������ڵ����������ʱ��Ϊ
| ��m |
| Bq |
| BqL |
| 2m |
��2���������������ij��ٶ���
| BqL |
| 2(2n+1)m |
| 1 |
| 2 |
| ��m |
| Bq |
����������Ҫͨ�����켣�����������˶���ʱ�䣬����������ѧ����������������������

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ��һ���̶��ľ�������ͨ�����Ȼ��������һ���������������壬����ͨ��������ת��ĸ�AB��Բ�̱�Ե���ӣ��뾶ΪR��Բ���ƹ̶�ת����O���Խ��ٶȦ���ʱ������ת�����γɻ���ˮƽ���������ͼʾλ����Բ��ת��90������У���������������
��ͼ��ʾ��һ���̶��ľ�������ͨ�����Ȼ��������һ���������������壬����ͨ��������ת��ĸ�AB��Բ�̱�Ե���ӣ��뾶ΪR��Բ���ƹ̶�ת����O���Խ��ٶȦ���ʱ������ת�����γɻ���ˮƽ���������ͼʾλ����Բ��ת��90������У���������������