题目内容
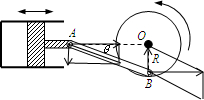
如图所示，一个固定的绝热汽缸通过绝热活塞封闭了一定质量的理想气体，活塞通过两端有转轴的杆AB与圆盘边缘连接，半径为R的圆盘绕固定转动轴O点以角速度ω逆时针匀速转动，形成活塞水平左右振动．则从图示位置起，圆盘转过90°过程中，汽缸内气体内能分析：根据B点的移动可得出A的移动，再根据热力学第一定律可得出汽缸内气体内能的变化；由运动的合成与分解的知识可得出AB杆的速度，再分析A点可得出活塞的速度．
解答：解；由图示位置转过90°的过程中，由图可知，B点右移，带动活塞右移，气体对外做功，由热力学第一定律可得，气体内能将减小；
在图示位置时，B点的合速度vB=ωR，沿切线方向；则沿AB杆的分速度为v1=
； 而在A点沿汽缸方向的分量v2=vcosθ； 故活塞的速度为ωR；
故答案为：减小；ωR
在图示位置时，B点的合速度vB=ωR，沿切线方向；则沿AB杆的分速度为v1=
| v |
| cosθ |
故答案为：减小；ωR
点评：本题将曲线运动和热学联系在一起，要求能正确的做好速度的分解，明确合运动与分运动的关系．
练习册系列答案
相关题目
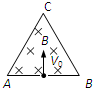
如图所示，一个固定的弹性等边三角形框架ABC，边长为L，在框内有垂直于纸面向里的匀强磁场，磁感应强度为B．在AB边的中点有一个小孔，现在有一个电量为+q、质量为m且不计重力的微粒，以某一初速度垂直于AB射入框内，微粒与框内壁垂直碰撞且能量与电量均不变，碰撞时间忽略不计，经过若干次这样的碰撞后又从入射点射出．求：
