��Ŀ����
����Ŀ����ͼ��ʾ�����⻬�������죬���d��2m���������ϵIJ�����ˮƽ�ģ������������дŸ�Ӧǿ��B��1T��������ֱ���µ��н�ų�������R��3���������H��0.8m��������ab����m��0.2kg�������r��1�����ӵ����Ͼ�����h��0.2m�ĸ߶ȴ��ɾ�ֹ�ͷţ���ص���������Ե��ˮƽ����s��0.4m��ȡg��10m/s2����
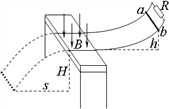
��1�������˸ս���ų�ʱ��R�ϵĵ�����С��
��2�����������е���R�ų���������
��3���ų�����Ŀ��ȡ�
���𰸡���1��1A��2��0.225J (3) 0.2m
����������1������ս���ų�ʱ�ٶ�Ϊv0���ɻ�е���غ㶨���У�mgh=![]() mv02
mv02
��ã�v0=2m/s
���ɷ����ڵ�Ÿ�Ӧ�����У�E=Bdv0=4V
�ɱպ�ŷķ�����У� ![]() ��
��
��2����������뿪�ų�ʱ�ٶ�Ϊv1���������뿪�ų���ƽ���˶�����ƽ���˶����ɣ�����ֱ����H=![]() gt2��
gt2��
��ˮƽ����s= v1t��
������ã�v1=1m/s��
���������غ㶨�ɣ����������л�·�����Ľ�����Q=![]() mv02-
mv02-![]() mv2��
mv2��
����R�ų�������QR=![]() Q ������ã�QR=0.225J��
Q ������ã�QR=0.225J��
��3����ų�����Ŀ���ΪL��������ͨ���ų�������ijһʱ�̵��ٶ�Ϊv���ڽ�������һ�κܶ�ʱ������t���ٶȱ仯Ϊ��v������ţ�ٵڶ����ɣ�
-F=ma=m![]() ��
��
F=BdI��I=![]() , E=Bd v ,
, E=Bd v ,
����ݶ���������- BdI��t=��p
��������-![]() v��t=m��v��
v��t=m��v��
��������������ͨ���ų��Ĺ��̣�-![]() ��v��t=m����v��
��v��t=m����v��
������v��t=L������v= v1- v0
������ã�L=0. 2m