题目内容
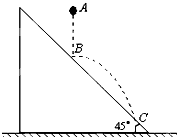 如图所示,从倾角为45θ的固定斜面B点正上方,距B点的高度为h的A点处,静止释放一个质量为m的弹性小球,落在B点和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间小球落在斜面上C点.空气阻力不计,重力加速度为g.则( )
如图所示,从倾角为45θ的固定斜面B点正上方,距B点的高度为h的A点处,静止释放一个质量为m的弹性小球,落在B点和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间小球落在斜面上C点.空气阻力不计,重力加速度为g.则( )分析:(1)根据匀变速直线运动的速度位移公式求出小球到达B点的速度,平抛运动的基本规律到达C点的竖直方向速度,求出重力瞬时功率.
(2)从B点反弹后做平抛运动,根据平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,求出运动的时间,求出竖直分速度,根据位移速度公式求解BC之间的高度差.
(2)从B点反弹后做平抛运动,根据平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,求出运动的时间,求出竖直分速度,根据位移速度公式求解BC之间的高度差.
解答:解:(1)小球下降过程中,做自由落体运动,落到斜面B点的速度为v,
满足:2gh=v2
解得:v=
然后小球以速度
做平抛运动,根据平抛运动的规律有:
tan45°=
解得;t=2
,故B错误,C正确;
所以到达C点时的竖直方向速度为:vy=gt=2
所以小球落到C点时重力的瞬时功率为mgvy=2mg
,故A错误;
HBC=
=4h,故D正确.
故选CD
满足:2gh=v2
解得:v=
| 2gh |
然后小球以速度
| 2gh |
tan45°=
| vt | ||
|
解得;t=2
|
所以到达C点时的竖直方向速度为:vy=gt=2
| 2gh |
所以小球落到C点时重力的瞬时功率为mgvy=2mg
| 2gh |
HBC=
| vy2 |
| 2g |
故选CD
点评:解答本题要知道平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,难度适中.

练习册系列答案
相关题目
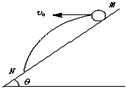 如图所示,从倾角为θ的斜面上的M点水平抛出一个小球.小球的初速度为v0,最后小球落在斜面上的N点,且重力加速度为g,由上述条件某同学试图求出
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球.小球的初速度为v0,最后小球落在斜面上的N点,且重力加速度为g,由上述条件某同学试图求出①小球什么时刻与斜面间的距离最大
②小球空中运动的时间
③M、N之间的距离
④小球落到N点时的速度大小和方向等4个量.那么你认为他最多可以求出其中的( )
| A、1个 | B、2个 | C、3个 | D、4个 |
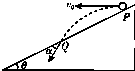 如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小 球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v0,则以下说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小 球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v0,则以下说法正确的是( )| A、小球在空中的运动时间变为原来的2倍 | B、夹角α将变大 | C、PQ间距等于原来间距的4倍 | D、夹角α与初速度大小无关 |
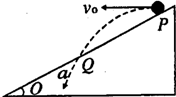 如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角为α,若把小球初动能变为2倍,则下列说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角为α,若把小球初动能变为2倍,则下列说法正确的是( )A、小球在空中运动时间变为原来的
| ||
| B、α角将变大 | ||
| C、PQ间距一定等于原来间距的4倍 | ||
| D、α角与初动能大小无关 |
 如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角α,若把小球初动能变为2倍,则下列说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角α,若把小球初动能变为2倍,则下列说法正确的是( ) 如图所示,从倾角为θ的足够长斜面顶端P以速度v0抛出一个小球,落在斜面上的点记作Q,小球落在斜面上的速度vt与斜面的夹角为α,若把初速度变为2v0,则( )
如图所示,从倾角为θ的足够长斜面顶端P以速度v0抛出一个小球,落在斜面上的点记作Q,小球落在斜面上的速度vt与斜面的夹角为α,若把初速度变为2v0,则( )