题目内容
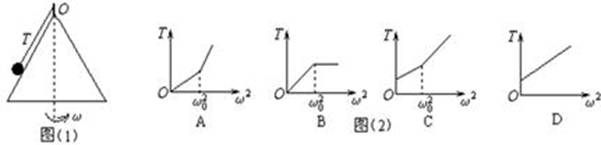
用一根细线一端系一小球(可视为质点),另一端固定在一光滑锥顶上,如图(1)所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图像是图(2)中的
【答案】
C
【解析】
试题分析:设绳长为L,锥面与竖直方向夹角为θ,当ω=0时,小球静止,受重力mg、支持力N和绳的拉力T而平衡,T=mgcosθ≠0,所以A项、B项都不正确;ω增大时,T增大,N减小,当N=0时,角速度为ω0.当ω<ω0时,由牛顿第二定律得,
Tsinθ-Ncosθ=mω2Lsinθ
Tcosθ+Nsinθ=mg
解得T=mω2Lsin2θ+mgcosθ
当ω>ω0时,小球离开锥子,绳与竖直方向夹角变大,设为β,由牛顿第二定律得
Tsinβ=mω2Lsinβ
所以T=mLω2
可知T-ω2图线的斜率变大,所以C项正确.
考点:匀速圆周运动的规律;牛顿定律。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
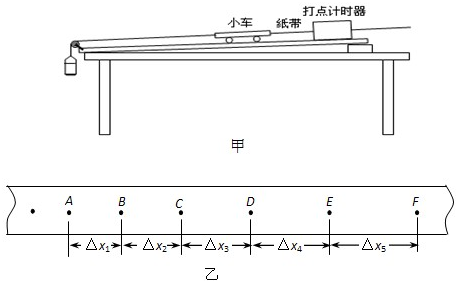
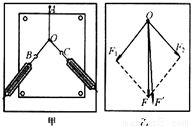
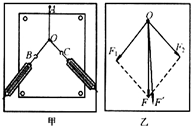 Ⅰ、在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某-点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉像皮条.
Ⅰ、在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,先用一个弹簧秤拉橡皮条的另一端到某-点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉像皮条.