题目内容
17. (1)在利用单摆测定重力加速度的试验中,若测得的g值偏大,可能的原因是BC.
(1)在利用单摆测定重力加速度的试验中,若测得的g值偏大,可能的原因是BC.A.直接将摆线长作为摆长
B.以摆线长、小球的直径之和作为摆长
C.测量周期时,把n个振动误认为(n+1)个全振动
D.测量周期时,把n个振动误认为(n-1)个全振动
(2)实验中秒表的示数如图1所示为99.5 s.
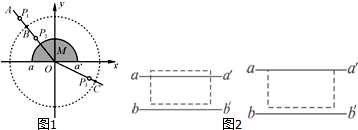
(3)该同学经测量得到6组摆长L和对应的周期T,画出T2-L图象,在图线上选取a、b两个点,坐标如图2所示.利用图象计算出当地重力加速度的表达式g=$\frac{4{π}^{2}({L}_{b}-{L}_{a})}{{{T}_{b}}^{2}-{{T}_{a}}^{2}}$.处理完数据后,该同学发现在计算摆长时将线长、小球的直径之和作为摆长,这样不会(选填“会”或“不会”)影响重力加速度的计算.
分析 (1)根据单摆的周期公式得出重力加速度的表达式,通过摆长和周期的测量误差分析重力加速度的误差.
(2)秒表的读数等于小盘读数加上大盘读数.
(3)根据单摆的周期公式得出T2-L的表达式,通过表达式,结合图线的斜率进行求解.
解答 解:(1)根据T=$2π\sqrt{\frac{l}{g}}$知,g=$\frac{4{π}^{2}l}{{T}^{2}}$,
A、直接将摆线长作为摆长,则摆长的测量值偏小,导致重力加速度的测量值偏小,故A错误.
B、以摆线长、小球的直径之和作为摆长,则摆长的测量值偏大,导致重力加速度的测量值偏大,故B正确.
C、测量周期时,把n个振动误认为(n+1)个全振动,则周期的测量值偏小,导致重力加速度的测量值偏大,故C正确.
D、测量周期时,把n个振动误认为(n-1)个全振动,则周期的测量值偏大,导致重力加速度的测量值偏小,故D错误.
故选:BC.
(2)秒表的小盘读数为90s,大盘读数为9.5s,则秒表的读数为99.5s.
(3)根据T=$2π\sqrt{\frac{L}{g}}$得:${T}^{2}=4{π}^{2}\frac{L}{g}$,
则斜率k=$\frac{4{π}^{2}}{g}=\frac{{{T}_{b}}^{2}-{{T}_{a}}^{2}}{{L}_{b}-{L}_{a}}$,解得:g=$\frac{4{π}^{2}({L}_{b}-{L}_{a})}{{{T}_{b}}^{2}-{{T}_{a}}^{2}}$.
根据数学知识,在计算摆长时用的是摆线长度而未计入小球的半径,这样不影响重力加速度的计算.
故答案为;(1)BC,(2)99.5,(3)$\frac{4{π}^{2}({L}_{b}-{L}_{a})}{{{T}_{b}}^{2}-{{T}_{a}}^{2}}$,不会.
点评 本题的关键由单摆的周期公式变形,得到T2与L的关系式得到图象斜率的物理意义,再分析实验产生的误差.

 阅读快车系列答案
阅读快车系列答案| A. | 1:2:3 | B. | 2:4:6 | C. | 1:4:9 | D. | 1:3:5 |
 如图所示,把一条通电导线平行地放在小磁针的上方附近时,小磁针会发生偏转.首先观察到这个实验现象的物理学家是( )
如图所示,把一条通电导线平行地放在小磁针的上方附近时,小磁针会发生偏转.首先观察到这个实验现象的物理学家是( )| A. | 奥斯特 | B. | 安培 | C. | 法拉第 | D. | 库仑 |
| A. | 飞船处于平衡状态 | |
| B. | 地球对飞船的万有引力提供飞船运行的向心力 | |
| C. | 飞船运行的速度小于第一宇宙速度 | |
| D. | 飞船运行的加速度小于地球表面的重力加速度 |
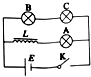 如图所示的电路中,L是一个电阻可忽略不计、自感系数很大的线圈,A、B、C为完全相同的三个灯泡.开始时电键K闭合,三个灯泡均发光,某时刻将电键K断开,则下列说法正确的是( )
如图所示的电路中,L是一个电阻可忽略不计、自感系数很大的线圈,A、B、C为完全相同的三个灯泡.开始时电键K闭合,三个灯泡均发光,某时刻将电键K断开,则下列说法正确的是( )| A. | 流经C灯的电流方向向右,A灯闪亮后缓慢熄灭 | |
| B. | 流经C灯的电流方向向左,B、C灯闪亮后缓慢熄灭 | |
| C. | 流经C灯的电流方向向右,B、C灯闪亮后缓慢熄灭 | |
| D. | 流经C灯的电流方向向左,B、C灯不会闪亮只是缓慢熄灭 |
| A. | 由抛出到落回抛出点的时间是3 s | |
| B. | 只有在2 s末时经过40 m高处 | |
| C. | 经过25 m高处时的瞬时速率只能是20 m/s | |
| D. | 上升的最大高度是90 m |
 如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )
如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )| A. | 向心力一定只由重力提供 | |
| B. | 受到杆的弹力不可能为零 | |
| C. | 若速率为$\sqrt{gl}$,则轻杆对小球有向上的支持力 | |
| D. | 若速率为$\sqrt{2gl}$,则轻杆对小球有向下的拉力 |
 如图所示,定值电阻R1=1Ω,R2为电阻箱,电源电动势e=6V,内阻 r=3Ω.要使电源有最大功率输出,应使R2=2Ω;若要使R1上得到的功率最大,应使R2=0;若要使R2上得到的功率最大,应使R2=4Ω.
如图所示,定值电阻R1=1Ω,R2为电阻箱,电源电动势e=6V,内阻 r=3Ω.要使电源有最大功率输出,应使R2=2Ω;若要使R1上得到的功率最大,应使R2=0;若要使R2上得到的功率最大,应使R2=4Ω.