题目内容
9.宇航员站在一星球表面上的某高处,沿水平方向抛出一个小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L,若抛出时的初速度增大到2倍,则抛出点与落地点之间的距离为$\sqrt{3}$L.已知两落地点在同一水平面上,该星球的半径为R,引力常量为G,则:(1)若在该星球上发射卫星,求最小的发射速度;
(2)该球星的平均密度为多大?
分析 (1)根据平抛运动的规律,知初速度增大到2倍,则水平位移也增大2倍,结合几何关系求出小球落地的高度,通过平抛运动竖直方向上的运动规律求出重力加速度的大小,结合万有引力等于重力求出月球的质量M,卫星做圆周运动,万有引力提供向心力,应用牛顿第二定律求出最小发生速度.
(2)应用密度公式求出星球的平均密度.
解答 解:(1)设抛出点的高度为h,第一次平抛运动的水平位移为x,则:x2+h2=L2
若抛出的初速度为2倍时,则水平位移为2x 因此有:(2x)2+h2=($\sqrt{3}$L)2
设该星球表面的重力加速度为g',则:h=$\frac{1}{2}$g′t2,
而在该星球表面上,有:G$\frac{Mm}{{R}^{2}}$=mg′,解得,星球质量:M=$\frac{2\sqrt{3}L{R}^{2}}{3G{t}^{2}}$;
万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,
解得:v=$\sqrt{\frac{2\sqrt{3}LR}{3{t}^{2}}}$;
(2)星球的平均密度:ρ=$\frac{M}{V}$=$\frac{\frac{2\sqrt{3}L{R}^{2}}{3G{t}^{2}}}{\frac{4}{3}π{R}^{3}}$=$\frac{\sqrt{3}L}{2πRG{t}^{2}}$;
答:(1)若在该星球上发射卫星,最小的发射速度是$\sqrt{\frac{2\sqrt{3}LR}{3{t}^{2}}}$;
(2)该球星的平均密度为$\frac{\sqrt{3}L}{2πRG{t}^{2}}$.
点评 本题综合考查了平抛运动和万有引力的综合,知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力等于重力这一理论,并能灵活运用.

 质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )
质量为m的物体从地面上方H高处无初速释放,落在地面后出现一个深度为h的坑,如图所示,在此过程中说法正确的是( )| A. | 外力对物体做的总功为零 | B. | 重力对物体做功为mg(H+h) | ||
| C. | 重力对物体做功为mgH | D. | 地面对物体平均阻力为$\frac{mg(H+h)}{h}$ |
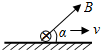 如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )
如图所示,一根长为L,质量为m的金属棒位于粗糙的水平面上,处在与水平方向成α角的匀强磁场中,0°<α<180°,金属棒与水平面的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,若在金属棒中通过以恒定电流I,在安培力作用下金属棒将向右做匀速运动,下列说法正确的是( )| A. | 当α=90°时安培力最小 | |
| B. | 当α=150°时磁感应强度最小 | |
| C. | 若磁感应强度大小为定值,在α<90°的前提下增大α,则金属棒将做匀减速运动 | |
| D. | 若磁感应强度大小为定值,在α<90°的前提下增大α,则金属棒将做加速运动 |
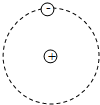 带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )
带负电量q的粒子绕固定的带正电Q的正电荷以速度v作顺时针方向的匀速圆周运动,粒子所在区间垂直圆周所在平面磁感应强度为B的匀强磁场,两电荷相距r,则( )| A. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | B. | 若Bqv<K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 | ||
| C. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向里 | D. | 若Bqv>K$\frac{Qq}{{r}^{2}}$,B可能垂直纸面向外 |
