题目内容
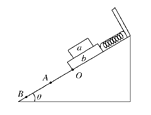
【题目】如图所示，有一个内壁光滑的圆锥形漏斗竖直放置，一个质量为m的小球在漏斗内壁某水平面内做匀速圆周运动。若漏斗的侧壁与竖直方向夹角为θ，小球运动的圆平面到漏斗底端的距离为h，则下列说法正确的是( )
A. 小球受到内壁的支持力与h无关，随θ的增大而增大
B. 小球运动的向心加速度与θ无关，随h的增大而增大
C. 小球运动的线速度与θ无关，随h的增大而增大
D. 小球运动的角速度与h无关，随θ的增大而增大
【答案】C
【解析】漏斗内壁母线与竖直方向的夹角为θ．以任意一个小球为研究对象，分析受力情况：重力mg和漏斗内壁的支持力N，它们的合力提供向心力，漏斗内壁的支持力
，即小球受到内壁的支持力与h无关，随θ的增大而减小，选项A错误；向心加速度
，即小球运动的向心加速度与θ有关，与h无关，选项B错误；根据牛顿第二定律得： 
，得到
，即小球运动的线速度与θ无关，随h的增大而增大，选项C正确； 角速度
，则小球运动的角速度与h有关，随θ的增大而减小，故D错误；故选C．
练习册系列答案
名校课堂系列答案
相关题目
